Контроль надежности по однократной выборке

Пусть необходимо проконтролировать надежность некоторой партии изделий. Требования к надежности каждого изделия заданы в следующем виде: изделие надежно, если вероятность его отказа Q в течение заданного времени t не превышает Q_o(t) и ненадежно, если Q(t)³Q₁(t). В процессе контроля требуется принять статистическое решение о том, являются изделия данной партии надежными или нет, и на этом основании принять или забраковать всю партию, обеспечив риск поставщика не более a, а риск заказчика не более b. Так как закон распределения наработки изделия Q(t) неизвестен, то, как и в случае определительных испытаний, выбираем план [N, Б, t], где длительность испытаний Т совпадает со временем t работы изделия в нормальной эксплуатации. Для проведения испытаний и принятия решения кроме Q_o и Q₁ необходимо знать еще четыре числа: риски a и b, объем партии N и приемочный норматив с. Если два из них задать, то два других можно определить по уравнениям (1) и (2).

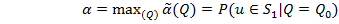(1)

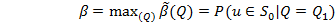(2)

Если задаются N и с, а определить нужно риски a и b, то получаем прямую задачу планирования контроля. Если же задаются a и b, а определить нужно N и с, то получаем обратную задачу планирования.

Найдем теперь явный вид уравнений (1) и (2). Поскольку число отказов изделий m за время испытаний t распределено по биномиальному закону, мы вместо (1) и (2) можем записать:

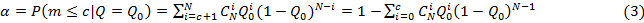
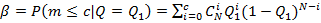(4)

В частности, при с = 0 имеем:

a=1-(1-Q₀)^N; b=1-(1-Q₁)^N

При с > 0 уравнения (3) и (4) можно решать с помощью таблиц биномиального распределения. Если же N велико, a Q мало, то можно воспользоваться пуассоновским приближением, тогда (1) и (2) заменяются следующими:

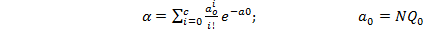(5)

(6)

При использовании приближения Большева—Смирнова значения а₀ и а₁, вычис-

ляются по формуле

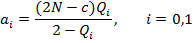
Дата добавления: 2014-01-04