
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вывод закона Стокса в главной системе координат
|
|
|
|
Вспомним, что в главных осях координат каждый из тензоров (2) принимает диагональный вид и содержит в общем случае по три величины. Естественно ожидать, что закон внутреннего трения жидкости не зависит от выбора системы координат, и вязкости должны быть инвариантными величинами относительно поворота осей координат в конкретной точке.
В главных осях координат (а Вы знаете, что главные оси тензора напряжения и тензора деформаций совпадают) искомых коэффициентов пропорциональности будет только 9. По этой причине вывод закона трения Стокса проведём сначала для главной системы координат, в ней определить коэффициенты будет проще, а лишь потом перенесём полученный результат на произвольную систему координат.
В главной системе координат (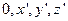 ) девиатор тензора напряжений
) девиатор тензора напряжений 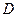 принимает диагональный вид.
принимает диагональный вид.
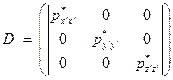 (8)
(8)
Как было уже отмечено, из всех величин, определяющих движение и напряжённое состояние жидкости (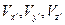 ,
, ,
,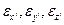 ,
,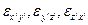 ), лишь три величины влияют на элементы девиатора тензора напряжений в главной системе координат. Это величины
), лишь три величины влияют на элементы девиатора тензора напряжений в главной системе координат. Это величины 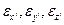 . Заметим, что скорости угловых деформаций
. Заметим, что скорости угловых деформаций 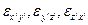 в главной системе координат равны нулю.
в главной системе координат равны нулю.
Следовательно, линейная зависимость напряжений девиатора от скорости угловых деформаций является прямо пропорциональной зависимостью напряжений 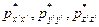 от скоростей угловых деформаций
от скоростей угловых деформаций 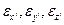 .
.
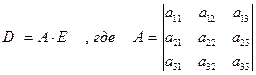
Запишем эти зависимости в общем виде:
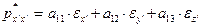 (9)
(9)
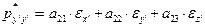 (10)
(10)
 (11)
(11)
Физический смысл каждого из коэффициентов 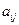 означает динамическую вязкость жидкости. В законе Ньютона для одномерного движения несжимаемой жидкости есть только один коэффициент пропорциональности – динамическая вязкость. А для трёхмерного пространства имеем девять вязкостей одной и той же жидкости при одной и той же температуре!
означает динамическую вязкость жидкости. В законе Ньютона для одномерного движения несжимаемой жидкости есть только один коэффициент пропорциональности – динамическая вязкость. А для трёхмерного пространства имеем девять вязкостей одной и той же жидкости при одной и той же температуре!
 На первый взгляд это кажется парадоксальным, так как мы привыкли иметь дело с однозначным определением динамической вязкости опытным путём с помощью вискозиметра, принцип действия которого основан на измерении времени протекания заданного объёма жидкости через трубку при заданной разнице давлений. Однако, коэффициенты могут и совпадать по величине, и поэтому сходу отказываться от дальнейших выкладок из-за кажущеёся абсурдности ситуации преждевременно.
На первый взгляд это кажется парадоксальным, так как мы привыкли иметь дело с однозначным определением динамической вязкости опытным путём с помощью вискозиметра, принцип действия которого основан на измерении времени протекания заданного объёма жидкости через трубку при заданной разнице давлений. Однако, коэффициенты могут и совпадать по величине, и поэтому сходу отказываться от дальнейших выкладок из-за кажущеёся абсурдности ситуации преждевременно.
Найти все девять коэффициентов (девять вязкостей) без ещё одного очень важного допущения мы не сможем.
Этим допущением является допущение об изотропности жидкости. До сих пор мы нигде не использовали это допущение. Теперь же в дальнейшем будем оговаривать, что все полученные ниже формулы имеют силу лишь для изотропных жидкостей, для которых можно считать все свойства независимыми от направления в пространстве. Очевидно, что это допущение не является обременительным, поскольку анизотропия свойственна лишь неньютоновским жидкостям, которые мы не рассматриваем, и жидким кристаллам.
Для изотропных жидкостей уравнения (9-11) сохраняются при любом выборе направлений координатных осей, то-есть коэффициенты 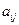 перед скоростями угловых деформаций должны сохранять свои значения при любом направлении координатных осей. Это так же естественно, как утверждать, что динамическая вязкость в законе трения Ньютона одинакова при движении жидкости в трубе в любом направлении: вправо, влево, вверх или вниз под углом. Воспользуемся свойством изотропии и запишем уравнения (9-11) в другой системе координат, где ось
перед скоростями угловых деформаций должны сохранять свои значения при любом направлении координатных осей. Это так же естественно, как утверждать, что динамическая вязкость в законе трения Ньютона одинакова при движении жидкости в трубе в любом направлении: вправо, влево, вверх или вниз под углом. Воспользуемся свойством изотропии и запишем уравнения (9-11) в другой системе координат, где ось 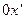 заменена на ось
заменена на ось 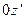 , а ось
, а ось 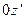 заменена на ось
заменена на ось 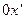 . Тогда уравнения (9-11) в новой системе координат примут вид:
. Тогда уравнения (9-11) в новой системе координат примут вид:
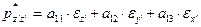 (12)
(12)
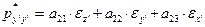 (13)
(13)
 (14)
(14)
Коэффициенты 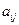 , стоящие перед скоростями угловых деформаций, например, перед
, стоящие перед скоростями угловых деформаций, например, перед 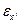 , должны быть одинаковыми в любой системе координат. Поэтому из сопоставления уравнений (9) и (14) следует:
, должны быть одинаковыми в любой системе координат. Поэтому из сопоставления уравнений (9) и (14) следует:
равенство коэффициентов перед 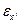 :
: 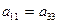 (15)
(15)
равенство коэффициентов перед 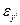 :
: 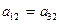 (16)
(16)
равенство коэффициентов перед 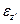 :
: 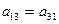 (17)
(17)
Запишем теперь уравнения (9-11) в системе координат, где ось 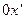 заменена на ось
заменена на ось  , а ось
, а ось  заменена на ось
заменена на ось 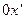 . Тогда уравнения (9-11) в этой системе координат примут вид:
. Тогда уравнения (9-11) в этой системе координат примут вид:
 (18)
(18)
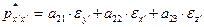 (19)
(19)
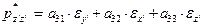 (20)
(20)
Из сопоставления уравнений (13) и (18) следует:
равенство коэффициентов перед 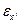 :
: 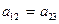 (21)
(21)
равенство коэффициентов перед 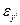 :
: 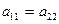 (22)
(22)
равенство коэффициентов перед 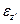 :
:  (23)
(23)
Из сопоставления уравнений (14) и (19) следует:
равенство коэффициентов перед 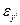 :
: 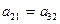 (24)
(24)
равенство коэффициентов перед 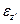 :
: 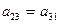 (25)
(25)
Подведём итоги:
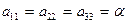 (26)
(26)
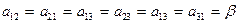 (27)
(27)
Исходные уравнения (9-11) принимают вид:
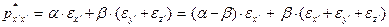 (28)
(28)
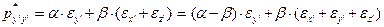 (29)
(29)
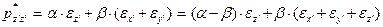 (30)
(30)
Для коэффициентов  и
и 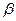 были введены новые обозначения:
были введены новые обозначения:
 (31)
(31)
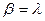 (32)
(32)
В новых обозначениях уравнения (28-30) принимают вид:
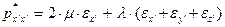 (33)
(33)
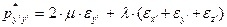 (34)
(34)
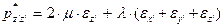 (35)
(35)
В развёрнутом виде с учётом уравнений (6) получаем закон трения Стокса в главной системе координат:
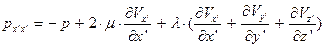 (36)
(36)
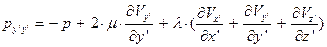 (37)
(37)
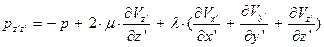 (38)
(38)
В законе трения Стокса коэффициент 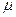 - это знакомая нам динамическая вязкость. Коэффициент
- это знакомая нам динамическая вязкость. Коэффициент 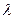 получил название второй или объёмной вязкости. Физическая природа второй вязкости долгое время оставался непознанной. Для несжимаемой жидкости, для которой дивергенция вектора скорости
получил название второй или объёмной вязкости. Физическая природа второй вязкости долгое время оставался непознанной. Для несжимаемой жидкости, для которой дивергенция вектора скорости 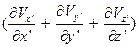 равна нулю, вторая вязкость не играет роли.
равна нулю, вторая вязкость не играет роли.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1883; Нарушение авторских прав?; Мы поможем в написании вашей работы!