
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доказательство. Ordm;. Углы Эйлера. Теорема Эйлера
|
|
|
|
Теорема Эйлера
Ordm;. Углы Эйлера. Теорема Эйлера
Теорема Эйлера. Построение матрицы ориентации твердого тела через углы Эйлера
Справедлива следующая теорема.
Любое положение ортов связанной системы координат может быть задано через векторные функции, зависящие не более чем от трех независимых угловых параметров.
Все элементы матрицы ориентации определяются через эти угловые параметры однозначно.
Не нарушая общности, можно считать, что полюсы абсолютной и связанной систем совпадают. Обозначим эти полюсы буквой 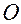 .
.
Рассмотрим наиболее общую ситуацию, когда оси связанной системы 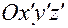 не совпадают с осями абсолютной системы
не совпадают с осями абсолютной системы 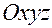 . Для определенности считаем, что
. Для определенности считаем, что 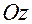 и
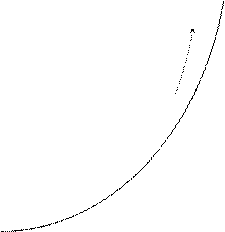
и 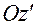 не совпадают (см. рис. 3.4.1).
не совпадают (см. рис. 3.4.1).
Обозначим 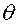 – угол между векторами
– угол между векторами  и
и  (
( и
и 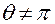 ). Далее введем следующие обозначения:
). Далее введем следующие обозначения:
 – орт линии пересечения плоскостей
– орт линии пересечения плоскостей 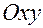 и
и 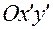 ;
;
эту линию назовем линией узлов;
 – орт линии пересечения плоскости
– орт линии пересечения плоскости 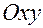
и плоскости 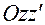 , перпендикулярной линии узлов;
, перпендикулярной линии узлов;
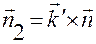 – орт линии пересечения плоскости
– орт линии пересечения плоскости 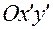
и плоскости 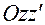 , перпендикулярной линии узлов.
, перпендикулярной линии узлов.
 |





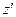
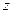

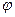
 |






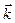
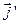



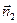


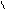

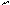












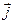
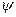

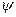
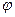
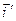

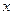
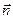
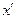
Рис. 3.4.1
Кроме угла 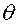 , введем углы (см. рис. 3.4.1):
, введем углы (см. рис. 3.4.1):
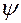 – угол, отсчитываемый в плоскости
– угол, отсчитываемый в плоскости 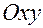 от орта
от орта 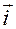 оси
оси 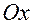
до орта 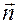 линии узлов; диапазон значений
линии узлов; диапазон значений 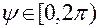 ;
;
угол 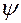 однозначно задает орт
однозначно задает орт 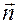 в плоскости
в плоскости 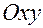
по формуле 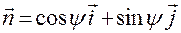 ;
;
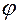 – угол, отсчитываемый в плоскости
– угол, отсчитываемый в плоскости 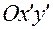 от орта
от орта 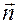 линии
линии
узлов до положительного направления оси 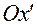 ,
,
т.е. до орта  ; диапазон значений
; диапазон значений 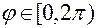 ;
;
угол 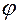 однозначно задает орт
однозначно задает орт 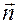 в плоскости
в плоскости 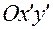
по формуле 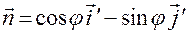 .
.
Напомним, что за положительное направление отсчета угла в ориентированной плоскости принято считать направление изменения этого угла против часовой стрелки, если смотреть на плоскость с конца орта нормали, задающего ее ориентацию.
Чтобы построить матрицу ориентации, надо выразить орты 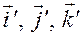 через сумму векторов
через сумму векторов  .
.
Запишем разложение векторов  ,
, 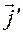 по векторам
по векторам 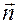 и
и 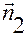 .
.


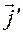
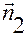


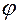




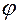
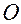
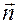
Рис. 3.4.2
Очевидно, 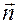 и
и 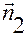 взаимно ортогональны; векторы
взаимно ортогональны; векторы 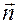 ,
, 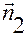 ,
,  ,
, 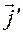 находятся в одной плоскости
находятся в одной плоскости 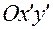 (см. рис. 3.4.2).
(см. рис. 3.4.2).
Орт 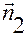 является направляющим вектором линии пересечения плоскостей
является направляющим вектором линии пересечения плоскостей 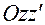 и
и 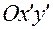 , а орт
, а орт 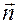 — направляющим вектором линии узлов (линии пересечения плоскостей
— направляющим вектором линии узлов (линии пересечения плоскостей 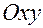 и
и 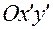 ).
).
Проектируя  ,
, 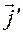 на орты
на орты 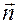 и
и 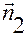 , получим
, получим

 , (3.4.1)
, (3.4.1)
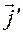
 . (3.4.2)
. (3.4.2)
Запишем разложение 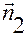 и
и  по векторам
по векторам 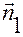 и
и  . Очевидно, орт
. Очевидно, орт 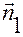 ортогонален
ортогонален  , орт
, орт 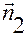 ортогонален
ортогонален  , и орты
, и орты 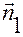 ,
, 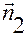 ,
,  ,
,  лежат в одной плоскости
лежат в одной плоскости 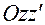 (см. рис. 3.4.3).
(см. рис. 3.4.3).


 |


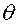
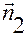
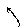
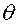

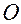
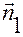
Рис.3.4.3
Орт 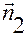 является направляющим вектором линии пересечения плоскостей
является направляющим вектором линии пересечения плоскостей 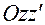 и
и 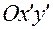 , а
, а 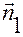 – направляющим вектором линии пересечения плоскостей
– направляющим вектором линии пересечения плоскостей 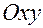 и
и 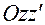 .
.
Проектируя 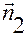 и
и  на орты
на орты 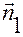 и
и  , найдем их разложение:
, найдем их разложение:
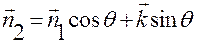 , (3.4.3)
, (3.4.3)
 . (3.4.4)
. (3.4.4)
Подставим (3.4.3) в (3.4.1) и (3.4.2):

 , (3.4.1)
, (3.4.1)
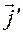
 . (3.4.2)
. (3.4.2)
Тогда вместе с (3.4.4) можем записать

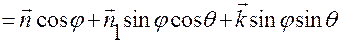 ,
,
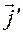
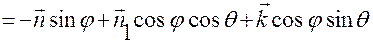 , (3.4.5)
, (3.4.5)
 .
.
Воспользуемся, наконец, тем, что векторы 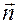 ,
, 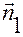 ,
, 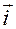 ,
,  находятся в одной плоскости
находятся в одной плоскости 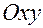 (см. рис. 3.4.4).
(см. рис. 3.4.4).
Орт 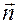 является направляющим ортом линии пересечения плоскостей
является направляющим ортом линии пересечения плоскостей 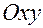 и
и 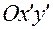 ;
; 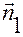 — направляющим ортом линии пересечения плоскостей
— направляющим ортом линии пересечения плоскостей 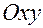 и
и 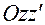 ; орты
; орты 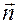 и
и 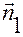 взаимно ортогональны.
взаимно ортогональны.
Проектируя 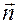 и
и 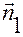 на орты
на орты 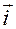 и
и 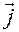 , будем иметь:
, будем иметь:
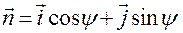 ,
, 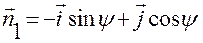 .
.
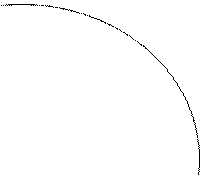
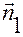
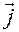

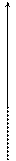

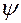
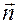
 |


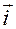
Рис. 3.4.4
Подставляя данные зависимости ортов 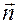 и
и 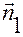 от
от 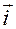 и
и 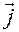 в (3.4.5), окончательно находим разложения векторов
в (3.4.5), окончательно находим разложения векторов 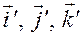 по ортам
по ортам  :
:
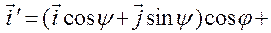
 ,
,

 ,
,
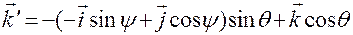 .
.
В них коэффициенты при ортах  в разложении
в разложении  (первое равенство) являются элементами первого столбца матрица
(первое равенство) являются элементами первого столбца матрица 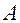 .
.
Аналогично, в разложении 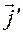 коэффициенты при ортах
коэффициенты при ортах  — элементы второго столбца, а в разложении
— элементы второго столбца, а в разложении  — третьего.
— третьего.
Таким образом, матрица 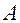 имеет вид:
имеет вид:
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 882; Нарушение авторских прав?; Мы поможем в написании вашей работы!