Метод Гольдфельда-Квандта

При малом объеме выборки, что наиболее характерно для эконометрических исследований, для оценки гетероскедастичности может использоваться метод Гольдфельда-Квандта, разработанный в 1965 r. Гольдфельд и Квандт рассмотрели однофакторную линейную модель, для которой дисперсия остатков возрастает пропорционально квадрату фактора. Для того чтобы оценить нарушение гомоскедастичности, они предложили параметрический тест, который включает в себя следующие шаги.

Шаг 1. Упорядочение n наблюдений по мере возрастания переменной х.

Шаг 2. Исключение из рассмотрения k центральных наблюдений; при этом (n – k) / 2 > р, где р – число оцениваемых параметров.

Шаг 3. Разделение совокупности из (n – k) наблюдений на две группы (соответственно с малыми и большими значениями фактора х) и определение по каждой из групп уравнений регрессии.

Шаг 4. Определение остаточной суммы квадратов для первой (S ₁) и второй (S ₂) групп и нахождение их отношения: F = S ₁ / S ₂, где S ₁ > S ₂.

При выполнение нулевой гипотезы о гомоскедастичности отношение F будет удовлетворять критерию с (n – k – 2 p) / 2 степенями свободы для каждой остаточной суммы квадратов. Чем больше величина F превышает табличное значение F -критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин.

Пример 3.9. Рассмотрим табл.3.7.

Таблица 3.7. Поступление доходов в консолидированный бюджет Санкт-Петербурга (у – млрд. руб.) в зависимости от численности работающих на крупных и средних предприятиях (х – тыс. чел.) и экономики районов за 1994 г.

№ п/п	Район города	xi	yi		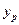ei
	Павловский		4,4	–1,0	5,4
	Кронштадт		8,1	2,5	5,6
	Ломоносовский		12,9	4,9	8,0
	Курортный		20,8	16,6	4,2
	Петродворец		15,5	19,0	–3,5
	Пушкинский		28,8	22,5	6,3
	Красносельский		37,5	41,4	–3,9
	Приморский		48,7	53,2	–4,5
	Колпинский		68,6	66,1	2,5
	Фрунзенский		104,6	82,6	22,0
	Красногвардейский		90,5	88,5	2,0
	Василеостровский		88,3	107,4	–19,1
	Невский		132,4	120,4	12,0
	Петроградский		122,0	127,4	–5,4
	Калининский		99,1	131,0	–31,9
	Выборгский		114,2	142,7	–28,5
	Кировский		150,6	151,0	–0,4
	Московский		156,1	171,0	–14,9
	Адмиралтейский		209,5	180,5	29,0
	Центральный		342,9	327,8	15,1
Итого		1855,5	1855,5	0,0

В соответствии с уравнением

; r = 0,9828, F = 510,7

найдены теоретические значения и отклонения от них фактических значений y, т.е. e_i. Остаточные величины e_i обнаруживают тенденцию к росту по мере увеличения х и y (рис.3.6).

Этот вывод подтверждается и по критерию Гольдфельда-Квандта. Для его применения сначала необходимо определить число исключаемых центральных наблюдений k. Из экспериментальных расчетов, проведенных авторами метода для случая одного фактора, рекомендовано при n = 30 принимать k = 8, а при n = 60 – соответственно k = 16. В рассматриваемом примере при n = 20 было отобрано k = 4. Тогда в каждой группе будет по 8 наблюдений [(20 – 4) / 2]. Результаты расчетов представлены в табл.3.8.

Рис.3.6. График остатков (для примера 3.9)

Таблица 3.8. Проверка линейной регрессии на гетероскедастичность

Уравнения регрессии	х	у		e	e^2
Первая группа с первыми 8 районами: ух = 2,978 + 0,921 x r = 0,979 F = 136,4		4,4	5,7	–1,3	1,69
	8,1	8,5	–0,4	0,16
	12,9	10,3	2,6	6,76
	20,8	19,6	1,2	1,44
	15,5	21,4	–5,9	34,81
	28,8	24,2	4,6	21,16
	37,5	38,9	–1,4	1,96
	48,7	48,1	0,6	0,36
Сумма					68,64
Вторая группа с последними 8 районами: yх= 31,142 + 1,338 x r = 0,969 F = 93,4		132,4	110,7	21,7	470,89
	122,0	118,7	3,3	10,89
	99,1	122,7	–23,6	556,96
	114,2	136,1	–21,9	479,61
	150,6	145,4	5,2	27,04
	156,1	168,2	–12,1	146,41
	209,5	178,9	30,6	936,36
	342,9	346,1	–3,2	10,24
Сумма		2639,31

Величина F = 38,45 (2639,31 / 68,64), что превышает табличное значение F -критерия = 4,28 при 5%-ном и 8,47 при 1%-ном уровне значимости для числа степеней свободы 6 для каждой остаточной суммы квадратов [(20 – 4 – 2 × 2) / 2], подтверждая тем самым наличие гетероскедастичности.

Критерий Гольдфельда-Квандта используется и при проверке остатков множественной регрессии на гетероскедастичность.

Дата добавления: 2014-01-04