Прием сигнала с QPSK

Теория оптимального приема говорит о том, что структура оптимального приемника при приеме M-ичного сигнала должна быть следующей:

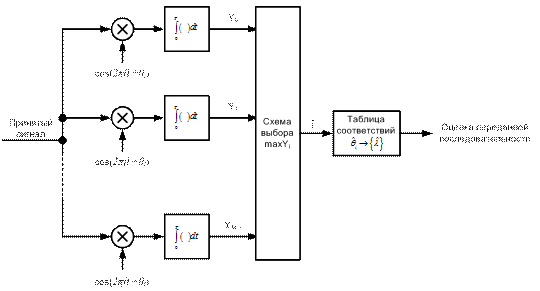
Рис. 1 Функциональная схема оптимального приемника М-ичного сигнала

Приемник должен сформировать М корреляционных интегралов принятого колебания со всеми возможными передаваемыми сигналами и принять решение в пользу сигнала, обеспечивающего наибольшее значение корреляции.

Однако для сигнала с дискретной ФМ эта схема является избыточной. Дело в том, что при фазовой манипуляции передаваемые сигналы различаются только значениями фазы, то есть величина корреляционного интеграла будет зависеть от разности фаз принимаемого и опорного сигнала коррелятора. При нулевом сдвиге корреляция будет максимальной, при сдвиге фазы на π – максимальной отрицательной, при сдвиге на π/2 - нулевой. Такую зависимость выходного сигнала коррелятора от разности фаз принимаемого и опорного сигналов можно использовать для построения более простого, но также оптимального по характеристикам приемника со схемой вида:

Рис. 2 Схема приемника-дискриминатора для приема QPSK сигнала

Работа этой схемы будет особенно простой для случая 4-QPSK. В этом случае достаточно определить знаки действительной и мнимой составляющих выходного сигнала приемника I* и Q*. Так, если I* > 0 и Q* > 0, это означает, что принятое колебание (точка в пространстве сигналов) находится в первом квадранте, то есть ближе всего к сигналу S₁₁ (смотри сигнальное созвездие). Если знаки I* < 0 и Q* > 0, это соответствует попаданию принятого колебания в четвертый квадрант и сигналу S₁₀ , и так далее.

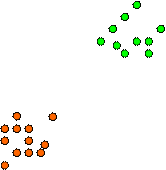
Рис. 3 Демодуляция QPSK-сигнала

Нетрудно заметить, что такое простое правило принятия решения получилось благодаря повороту созвездия 4-ФМ сигнала на π/4, в результате чего все точки созвездия QPSK оказались в диагоналях квадрантов. В результате, все точки, попавшие в данный квадрант, автоматически оказываются ближе всего к соответствующей точке сигнального созвездия рис.75.

Вероятность ошибок при приеме QPSK-сигнала можно определить следующим образом.

Во-первых, при четверичном приеме имеют место ошибки в сторону одного из трех альтернативных сигналов (смотри рис. 3). При этом, вероятность ошибки в сторону двух сигналов одинакова, а в сторону третьего – более удаленного, несколько меньше. В результате можно получить выражение:

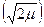Р_ОШQPSK = 2·(1 - Ф ) + (1 - Ф ) (1)

где Ф (z) – табулированный интеграл вероятности (или функция ошибок), m = E / N ₀ - энергетическое ОСШ на входе приемника.

Второе слагаемое в этом выражении будет существенно меньше первого, поэтому можно полагать, что

Р_ОШQPSK = 2·(1 - Ф ) (2)

То есть, вероятность ошибок при использовании QPSK будет все-таки выше, чем при двоичной фазовой манипуляции (сигналов больше и они ближе друг к другу).

Еще большей будет вероятность ошибок при использовании восьмиричной фазовой манипуляции (8-PSK) с сигнальным созвездием вида рис. 4. Для такой модуляции сигналы в созвездии расположены еще ближе друг к другу, и вероятность того, что при передаче одного сигнала будет принято решение о том, что передавался какой-либо другой сигнал, будет еще большей.

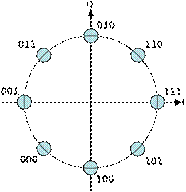
Рис. 4 Пространство сигналов для 8-PSK

На рис. 5 приведены полученные расчетным путем зависимости вероятности ошибок (BER) от ОСШ в канале связи для различных видов фазовой манипуляции – QPSK, 8-PSK и 16-PSK. Видно, что с увеличением кратности модуляции (и соответствующим увеличением удельной скорости передачи - бит/с∙Гц), увеличивается вероятность ошибок.

Соответственно, для сохранения неизменной вероятности ошибок требуется существенное увеличение отношения сигнал/шум в канале связи. Это говорит о том, что фазовую манипуляцию с высокой кратностью можно использовать только при наличии высокого энергетического потенциала в канале связи.

Рис. 5 Зависимость вероятности ошибки от ОСШ

Таким образом, многопозиционная фазовая модуляция – M-PSK, хотя и обладает высокой спектральной эффективностью, но с увеличением кратности модуляции М сильно теряет в помехоустойчивости, то есть может использоваться только в каналах с хорошим отношение сигнал/шум, например – в кабельных сетях DVB-C.

2. Квадратурная амплитудная модуляция – КАМ (QAM)

Квадратурно-амплитудная модуляция (КАM, QAM) представляет собой дальнейшее развитие фазовой модуляции (M-PSK).

Как мы только что показали, фазовая модуляция может быть представлена как сумма двух амплитудно-модулированных сигналов (I-канал и Q-канал), которые при сложении в канале дают фазово-модулированный сигнал.

Этот способ, названный способом квадратурного представления фазомодулированного сигнала, может быть продолжен, когда каждый из квадратурных каналов независимо друг от друга модулируется еще и по амплитуде. Таким образом, изменяются уже две координаты сигнала - фаза и амплитуда.

На фазовой плоскости такой сигнал отображается точками, расположенными в плоскости в соответствии с фазой и амплитудой сигнала. Сигнальное созвездие для модуляции 16-КАМ показано на рис. 6. При этом амплитуды сигналов в каждом из каналов могут принимать 4 значения (± 2 уровня), а их комбинация с 4-мя возможными значениями фазы дает 16 различных значений сигнала. Таким образом, при использовании 16-КАМ одним сигналом можно одно из 16-ти значений сообщения, или 4 бита. Другими словами, удельная скорость передачи при использовании 16-КАМ составит 4 (бит/с∙Гц).

Рис. 6. Сигнальное созвездие 16-КАМ

Существует несколько способов практической реализации 16-КАМ, наиболее распространенным из которых является так называемый способ модуляции наложением (SPM — Supersposed Modulation). При этом фактически реализуется два одинаковых модулятора 4-QPSK с амплитудами сигнала, различающимися в два раза. Структурная схема модулятора SPM и диаграммы, поясняющие его работу приведены на рис. 7.

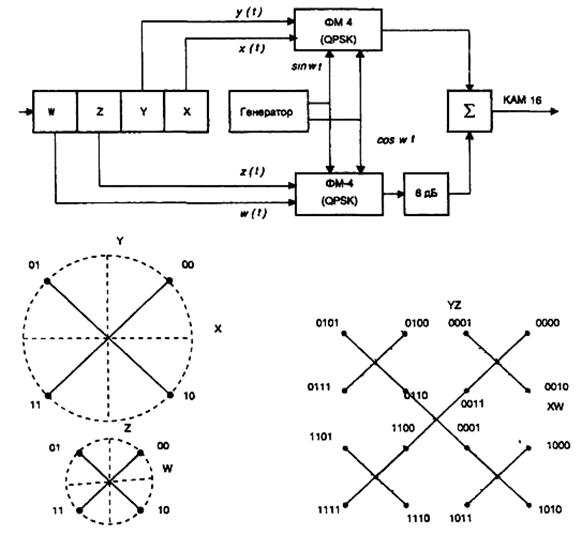
Рис. 7. Функциональная схема модулятора 16-КАМ на основе SPM

Аналогичным образом можно осуществлять квадратурную амплитудную модуляцию и с более высокой кратностью - 32-КАМ, 64-КАМ и т.д.

В настоящее время уже используются 64-КАМ (в этом случае удельная скорость передачи составляет 6 (бит/с∙Гц), в перспективе внедрение 128-КАМ и 256-КАМ с удельной скоростью 7 и 8 (бит/с∙Гц). Это позволяет значительно увеличить пропускную способность каналов связи, или же, сузить полосу канала при сохранении скорости передачи. Это особенно существенно для кабельных сетей, где энергетика канала хорошая и нужно постараться по существующим сетям передать как можно больше ТВ каналов.

Прием сигнала с М-КАМ производится так же, как и при М-ФМ (смотри рис. 74), при этом учитывается не только фаза (соотношение между I и Q), но и амплитуда сигнала - Q2 +I2.

Вероятность ошибок при использовании М-КАМ. Помехоустойчивость системы с КАМ определяется числом точек в сигнальном созвездии и расстоянием между ними. При большом числе точек сигналы системы КАМ имеют несколько лучшие характеристики, чем системы ФМ. Основная причина этого состоит в том, что расстояние между сигнальными точками в системе КАМ больше расстояния между сигнальными точками в системе ФМ.

Дата добавления: 2014-01-04