Интенсивность переходов

Интенсивность перехода І₁₂ пропорциональна квадрату модуля момента перехода, т.е. І₁₂ ~ ½М₁₂½², а сам момент перехода М₁₂ (или переходный момент) определяется равенством: М₁₂ = òχ₁Mχ₂dτ, где χ₁ и χ₂ – колебательные волновые функции основного и возбужденного состояния, М – оператор дипольного момента М. Последний в свою очередь описывается равенством: М = åе_іr_i, где e_i – заряд і-й частички (электрон, ядро), r_i – векторное расстояние от центра тяжести молекулы до і-й частички, dτ – элементарный объем многомерного пространства.

Оператор дипольного момента М как вектор может быть разложен на три составляющие по трем координатам:

М = М_х + М_у + М_z.

Тогда вектор переходного момента в свою очередь разлагается на три компонента:

М₁₂ = М₁₂^x + М₁₂^y + М₁₂^z_­=òχ₁M_xχ₂dτ + òχ₁M_yχ₂dτ + òχ₁M_zχ₂dτ.

Если M₁₂ ¹ 0 – переход разрешен и интенсивность І > 0. Если же M₁₂ = 0, то переход запрещен и интенсивность І=0. Переходный момент M₁₂ будет равным нулю, если все три его компоненты, М₁₂^x, М₁₂^y и М₁₂^z_­, равны 0, если же хотя бы одна из них оказалась не равной 0, то переход становится разрешенным.

То обстоятельство, равен или не равен интеграл от подинтегральной функции нулю, зависит от симметрии подинтегральной функции. Если взять в качестве симметричной функции у = х², то интеграл от нее (площадь под кривой, см. ниже рис.А) положителен и больше нуля:

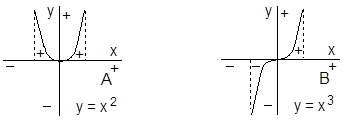
Если же взять нечетную (асимметричную) функцию у = х³ (график В). то обе половинки площади под кривой имеют противоположные знаки и взаимно компенсируются и интеграл от такой функции равен 0. Отсюда вывод: интеграл от симметричной функции всегда больше нуля, интеграл от антисимметричной функции всегда равен нулю.

11.2.1. Правила отбора по симметрии колебательной волновой функции χ.

Как было показано в разделе 10.2.2 (лекция № 10), χ_o, χ₂, χ₄ – cимметричные функции, χ₁, χ₃ и т.д. – имеют симметрию колебательной координаты x (т.е. симметрию нормального колебания), М_x, М_y, М_z – cимметрию движения вдоль координат х, y и z для той точечной группы, к которой принадлежит рассматриваемая молекула.

Пример: переход 0®1 для Н₂О.

11.2.1.1. Колебание ν₁ = ν_s.

Здесь χ₁=A₁, χ₂=A₁, M_x=B₁, M_y=B₂, M_z=A₁. M₁₂=òA₁B₁A₁dτ + òA₁B₂A₁dτ + òA₁A₁A₁dτ = òB₁dτ + òB₂dτ + òA₁dτ = М₁₂^x(=0) + М₁₂^y(=0) + М₁₂^z_­(¹0) ¹ 0, переход разрешен, поскольку М₁₂^z_­ ¹ 0.

11.2.1.2. Колебание ν₂ = ν_as.

Здесь, χ₁=A₁, χ₂=В₂ . M₁₂=òA₁B₁В₂dτ + òA₁B₂В₂dτ + òA₁A₁В₂dτ = òА₂dτ + òА₁dτ + òВ₂dτ = М₁₂^x(=0) + М₁₂^y(¹0) + М₁₂^z_­(=0) ¹ 0, переход разрешен, поскольку М₁₂^y ¹ 0.

11.2.1.3. Колебание ν₃=δ.

Здесь χ₁=A₁, χ₂=A₁ . Ситуация та же самая, что и в случае колебания ν₁: переход разрешен, поскольку М₁₂^z_­ ¹ 0.

11.2.2. Правила отбора по квантовому числу v.

Переходы разрешены, если Δv= + 1, т.е. разрешены переходы между соседними колебательными уровнями: 0®1, 1®2, 2®3. При этом необходимо учитывать, что вследствие заселенности наиболее интенсивным будет переход 0®1, переходы 1®2 примерно в 100 раз менее интенсивны, поскольку на первом уровне находится примерно 1 % от всех молекул. Переходы с еще более высоких колебательных уровней, для которых v ³ 2, в виду очень малой заселенности этих уровней в ИК спектрах практически не наблюдаются.

Запрещены переходы 0®2, 0®3, 1®3 и т.д., частоты которых примерно удвоены, утроены. Называются такие переходы обертонами (музыкальный термин).

Следует отметить, что обратный излучательный переход 1® 0 + hn запрещен, ибо его вероятность достаточно мала, чтобы успел осуществиться другой, безизлучательный переход, когда избыток колебательной энергии вследствие частого столкновения молекул передается на решетку, т.е. превращается в тепловую энергию движения.

11.2.3. Правила отбора по числу возбуждаемых колебаний.

Этим правилом разрешаются переходы, при которых только одно колебание изменяет квантовое число v. Запрещены переходы, при которых возбуждается сразу несколько колебаний, т.е. одновременно изменяются колебательные квантовые числа для нескольких колебаний. Примером проявления таких запрещенных переходов является появление в ИК-спектрах мало интенсивных составных (n₁ + n₂) и разностных (n₂ - n₁) частот.

Дата добавления: 2014-01-04