Примеры колебаний других молекул

11.3.1. НСl (C_¥v), 3N – 5=1.

Тип симметрии колебания А₁, M_z=A₁; таким образом, M₁₂^z=òA₁A₁A₁dτ =òA₁dτ ¹0, переход разрешен.

11.3.2. N₂ (D_{¥ h}), 3N – 5=1.

Тип симметрии колебания А_1g, M_x = M_y =E_u , M_z=A_1u, M₁₂=0, ибо М₁₂^x =М₁₂^y =òA_1gE_uA_1gdτ=òE_udτ = 0; M₁₂^z =òA_1gA_1uA_1gdτ =òA_1udτ = 0, переход запрещен.

11.3.3. H-CºC-H (D_{¥ h}), 3N – 5 = 7.

ν₁=ν_s(C-H) H-CºC-H

Тип симметрии колебания А_1g,

ν ₂= ν_s (CºC) H-CºC-H переход запрещен.

ν ₃=ν_as(C-H) H-CºC-H Тип симметрии колебания А_1u, переход разрешен,

ибо M_z=A_1u, M₁₂^z ¹ 0.

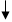
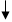ν₄=ν₅ = δ₁ H-CºC-H Тип симметрии E_g, переход запрещен, ибо

M­_x, M_y и M_z не принадлежат к этому типу.

ν₆=ν₇ = δ₂ H-CºC-H Тип симметрии E_u, к нему принадлежат М_х и

М_y, переход разрешен.

Колебания δ₁ и δ₂ дважды вырождены, те. Их по два.

Из приведенных здесь примеров видно, что разрешены те колебания, при которых дипольный момент молекулы изменяется, т.е. в данном случае ¶m/¶r ¹ 0. В тех же случаях, когда ¶m/¶r = 0, переходы запрещены.

11.4. Групповые колебания.

Пример: СН₃-СºСН та НСºСН, Δν(СºС)=170 см^-1. Колебание связи СºС в ацетилене не затрагивает других связей и является строго индивидуальным. Наблюдаемое же различие между частотами колебаний в метилацетилене и ацетилене не может быть объяснено индуктивным эффектом метильной группы. Расчеты по определенным методикам показывают, что в метилацетилене меняется сам характер движения, в котором принимают участие все связи молекулы, причем, смешиваются два типа колебаний, и валентные и деформационные с участием углов между С-Н связями группы СН₃.

Называют такие колебания групповыми или смешанными. Следует отметить, что в ИК-спектроскопии чисто валентные колебания одной связи встречаются очень редко, чаще всего имеют место групповые колебания, где колебания той или иной связи в той или иной мере преобладают. И чем сильнее имеет место это преобладание, тем характеристичнее это колебание является.

Дата добавления: 2014-01-04