Методом наибольшего правдоподобия

Алгоритм оценки параметра распределения

1. Построить функцию правдоподобия .

2. Определить логарифмическую функцию правдоподобия .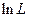

3. Найти .

4. Определить критические точки производной из решения уравнения

. (14.15)

5. Вычислить в найденных точках. Если , то при значении параметра 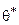функция 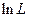имеет максимум, если 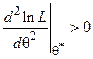, то при значении параметра 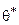функция 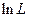имеет минимум.

6. Значение параметра 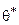, при котором функция 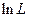достигает максимума, принимается за величину оцениваемого параметра.

Пример 14.5. По выборке 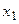, ,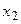..., методом наибольшего правдоподобия найти точечную оценку параметра 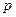геометрического распределения 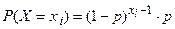, где 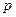− вероятность появления события в отдельном испытании.

Решение. Составим функцию правдоподобия

.

Получим логарифмическую функцию правдоподобия

.

Найдем критические точки логарифмической функции правдоподобия

,

,

,

,

,

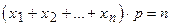т.е. логарифмическая функция правдоподобия имеет единственную критическую точку .

Определим наличие и характер экстремума логарифмической функции правдоподобия в этой точке. Найдем выражение второй производной

.

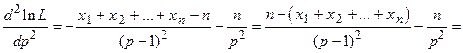
Тогда . Определим знак числителя

,

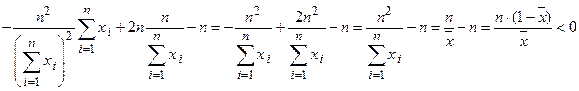так как . Поэтому .

Таким образом, при значении параметра распределения логарифмическая функция правдоподобия достигает максимума.

Ответ. .

Пример 14.4 (продолжение). Найти точечную оценку неизвестного параметра 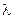методом наибольшего правдоподобия.

Решение. Составим функцию правдоподобия

.

Получим логарифмическую функцию правдоподобия

.

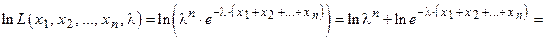
Найдем критические точки логарифмической функции правдоподобия:

,

, , .

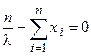Таким образом, логарифмическая функция правдоподобия имеет единственную критическую точку .

Определим наличие и характер экстремума логарифмической функции правдоподобия в этой точке

при .

Это означает, что в указанной критической точке логарифмическая функция правдоподобия имеет максимум.

Ответ. .

Замечание 14.1. Если методом наибольшего правдоподобия требуется определить оценки 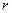параметров, то соответствующая закону распределения функция правдоподобия (14.13) или (14.14) будет содержать параметры 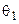, ,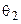..., . 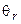Условие (14.15) примет вид системы из 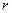уравнений

. (14.16)

Таким образом, метод наибольшего правдоподобия сводится к нахождению максимума функции одного или нескольких оцениваемых параметров.

Дата добавления: 2014-01-04