Интервальные оценки параметров нормального закона распределения

Точечная оценка 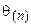является лишь приближенным значением неизвестного параметра 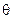даже в том случае, если она несмещенная, состоятельная и эффективная, и для выборки малого объема может существенно отличиться от истинного значения параметра .

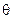Чтобы получить представление о точности и надежности оценки 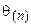параметра 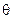можно использовать интервальную оценку.

Определение 14.8. Интервал , в который оцениваемый параметр 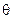попадает с заданной вероятностью 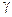, называется доверительным, а 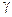− доверительной вероятностью (надежностью) оцениваемого параметра 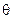, т.е.

.

Число называется уровнем значимости.

Величина доверительного интервала существенно зависит от объема выборки (уменьшается с ростом 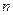) и от значения доверительной вероятности 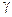(увеличивается с приближением 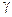к единице).

Пусть имеется нормально распределенная по группировочному количественному признаку генеральная совокупность (СВ 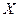). Если известно среднее квадратичное отклонение 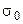, то определение доверительного интервала для математического ожидания происходит по следующему правилу. На основании результатов выборки объемом 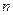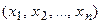рассчитывается . Задается доверительная вероятность 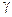. По таблице значений функции Лапласа определяется аргумент 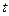, при котором .

Требуемый интервал задается неравенствами:

, (14.17)

где 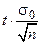− предельная ошибка выборки, − средняя ошибка выборки.

Действительно, из курса теории вероятностей известна оценка

.

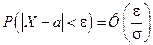Тогда для отклонения выборочной средней от математического ожидания (генеральной средней) можно записать равенство

,

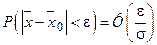учитывая 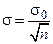и обозначив , получим 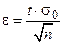. Тогда оцениваемые неравенства примут вид: или

.

Если 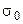неизвестно, то для определения доверительных интервалов используют 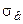. Предварительно следует найти 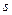по формуле . Тогда

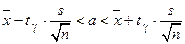, (14.18)

где определяют из таблицы «Критические точки распределения Стьюдента» по заданному уровню значимости , где , при числе степеней свободы .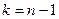

Доверительный интервал для 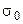определяется по исправленному среднему квадратичному отклонению на основании формул

(14.19)

где − параметр, определяется из соответствующего приложения .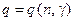

Действительно, рассмотрим равенство . Тогда

,

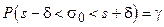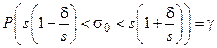
и, обозначив через 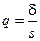, придем к интервальным оценкам (14.19).

Пример 14.6. Найти минимальный объем выборки, при котором с надежностью 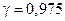точность оценки математического ожидания 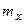генеральной совокупности по выборочному среднему равна , если известно среднее квадратичное отклонение генеральной совокупности 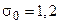, распределенной нормально.

Решение. Формула для определения доверительного интервала математического ожидания нормально распределенной совокупности имеет вид

,

где точность оценки математического ожидания 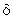представляет собой предельную ошибку .

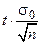Так как значение 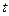, при котором , в данном случае составляет 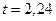, то получаем , откуда 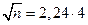, . Так как объем выборки – натуральное число, то .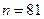

Заметим, что при использовании табулированных значений функции Лапласа вида 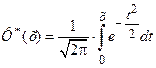, значение следует определять из условия 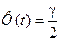. В данном случае .

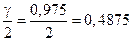Ответ. .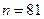

Дата добавления: 2014-01-04