
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Замечания
|
|
|
|
1. Обозначим  . Как следует из (3.12.2)
. Как следует из (3.12.2)
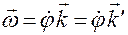 , (3.12.2)
, (3.12.2)
 , и справедливы неравенства
, и справедливы неравенства  при
при 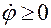 и
и 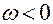 при
при 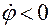 .
.
Величина 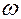 является скоростью изменения угла
является скоростью изменения угла 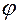 . Поэтому вектор
. Поэтому вектор 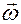 , построенный при изучении вращения твердого тела вокруг неподвижной оси, получил название вектор мгновенной угловой скорости.
, построенный при изучении вращения твердого тела вокруг неподвижной оси, получил название вектор мгновенной угловой скорости.
Такое же название дано тому вектору 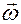 , который вычисляется по формуле (3.12.7)
, который вычисляется по формуле (3.12.7)
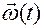
 (3.12.7)
(3.12.7)
на движениях тела, отличных от вращения вокруг неподвижной оси, а также на движениях других механических систем и подвижных систем координат.
Однако следует заметить, что при рассмотрении движений общего характера данное название вектора 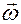 нельзя увязывать с существованием какого-либо угла, по скорости изменения которого можно было бы судить о модуле этого вектора.
нельзя увязывать с существованием какого-либо угла, по скорости изменения которого можно было бы судить о модуле этого вектора.
2. Из доказательства теоремы следует, что твердое тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы.
Действительно, положение 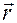 любой точки
любой точки 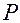 твердого тела относительно фиксированной точки
твердого тела относительно фиксированной точки 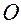 , находящейся на оси вращения, определяется по формуле
, находящейся на оси вращения, определяется по формуле  .
.
Здесь 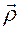 — положение точки
— положение точки 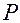 в связанной системе координат.
в связанной системе координат.
Как показано в теореме, матрица ориентации 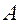 полностью определена в любой момент времени
полностью определена в любой момент времени  , если в этот момент известен угол поворота
, если в этот момент известен угол поворота 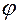 твердого тела вокруг неподвижной оси. Таким образом, для определения положения тела необходимо и достаточно знать одну угловую координату
твердого тела вокруг неподвижной оси. Таким образом, для определения положения тела необходимо и достаточно знать одну угловую координату 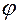 .
.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 303; Нарушение авторских прав?; Мы поможем в написании вашей работы!