
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Случайные векторы
|
|
|
|
Лекция № 13
| Тема: | Распределение случайного вектора. Независимость случайных величин. Распределение функций от случайных величин |
Пожалуй, нет ни одной отрасли математики такой интересной, такой важной, как теория вероятностей. История ее открываеи чудеса, которых может достич математическая наука, и пределы, которые она не может преступить.
Э. Девис
| Определение 13.1 | Случайным вектором 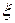 со значениями в со значениями в 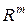 называется последовательность называется последовательность 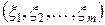 действительных случайных величин действительных случайных величин 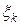 , , 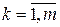 , определенных на одном вероятностном пространстве , определенных на одном вероятностном пространстве 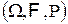 . Величина . Величина 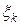 , , 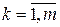 называетсяk–ой координатой вектора называетсяk–ой координатой вектора 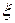 . .
|
Так как 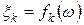 , здесь
, здесь 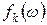 —
— 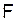 –измеримая действительная функция, то
–измеримая действительная функция, то 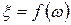 , где
, где 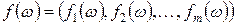 — функция со значениями в
— функция со значениями в 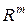 с
с 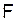 –измеримыми координатами. Эта функция отображает пространство
–измеримыми координатами. Эта функция отображает пространство 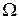 в
в 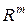 . Для каждого множества
. Для каждого множества 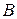 из
из 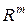 положим
положим
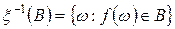 .
.
Для каждого борелевского множества 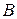 из
из 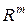
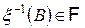 . Следовательно, определена вероятность
. Следовательно, определена вероятность 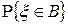 .
.
Пусть
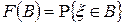 ,
, 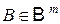 .
.
Функция множеств 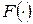 является мерой, причем
является мерой, причем 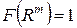 .
.
| Определение 13.2 | Меру 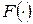 , определенную на , определенную на 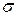 –алгебре борелевских множеств –алгебре борелевских множеств 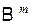 называютраспределением случайного вектора называютраспределением случайного вектора 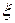 . .
|
| Определение 13.3 | Функцией распределения 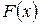 случайного вектора случайного вектора 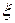 или совместной функцией распределения последовательности случайных величин или совместной функцией распределения последовательности случайных величин 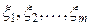 называют функцию: называют функцию:
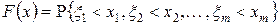 . .
|
Подобно тому, как это было сделано в одномерном случае, для многомерных функций распределения можно установить свойства:
I) 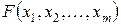 суть неубывающая функция по каждому аргументу;
суть неубывающая функция по каждому аргументу;
II) 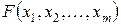 — непрерывная слева функция по каждому аргументу;
— непрерывная слева функция по каждому аргументу;
III) 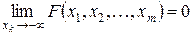 ,
, 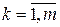 ;
;
IV) 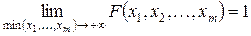 .
.
Как мы знаем, в одномерном случае перечисленные свойства являлись необходимыми и достаточными того, чтобы функция 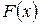 была функцией распределения некоторой случайной величины. В многомерном случае необходимо дополнительное условие — условие согласованности.
была функцией распределения некоторой случайной величины. В многомерном случае необходимо дополнительное условие — условие согласованности.
Введем в рассмотрение конечно–разностный оператор 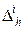 , действующий на функцию
, действующий на функцию 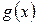 следующим образом:
следующим образом:
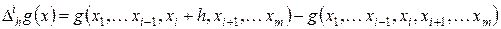 ,
, 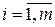 .
.
| Теорема 13.1. | Пусть 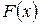 , , 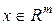 , — произвольная функция, удовлетворяющая условиям I, II, III,IV а также
V) для любых , — произвольная функция, удовлетворяющая условиям I, II, III,IV а также
V) для любых 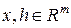
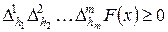 ,
тогда существует вероятностное пространство ,
тогда существует вероятностное пространство 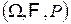 и случайная вектор и случайная вектор 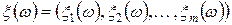 на нем такой, что функция распределения на нем такой, что функция распределения 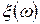 равна равна 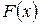 . .
|
Пример 13.1. Покажем, что требование V может быть не выполнено, несмотря на наличием у функции 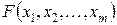 свойств I–IV. Пусть
свойств I–IV. Пусть
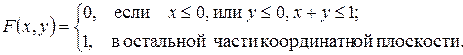
Не трудно видеть, что эта функция удовлетворяет условиям I–IV, но для нее
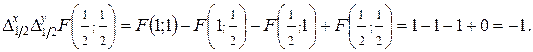
И, следовательно, пятое требование не выполнено.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 713; Нарушение авторских прав?; Мы поможем в написании вашей работы!