Коэффициент скольжения

Коэффициент скольжения учитывает влияние геометрических и кинематических параметров на величину проскальзывания, а, следовательно, и износа профилей зубьев в процессе зацепления.

При зацеплении двух колес профиль одного зуба перекатывается со скольжением по профилю другого зуба. Наличие скольжения при одновременном нажатии одного профиля на другой приводит к износу профилей.

Величина проскальзывания профилей характеризуется коэффициентом скольжения.

	Дуги перекатываются одна по другой со скольжением за время Δt. Эти дуги разные по длине. Разность длин дуг профилей зубьев, находящихся в контакте за малый промежуток времени Δt составляет дугу скольжения.

Коэффициенты скольжения для шестерни и зубчатого колеса определяются выражениями

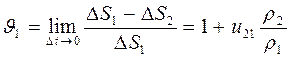
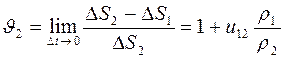
где 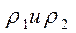радиусы кривизны в точке контакта (К) профилей зубьев первого и второго колеса. С учётом того, что передаточное отношение можно

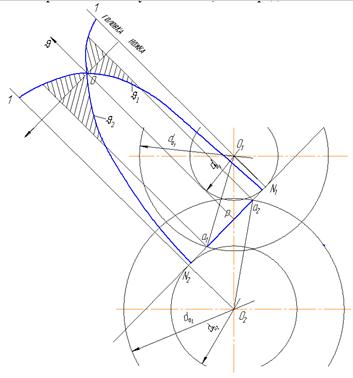
определить через радиусы начальных окружностей колёс, а радиусы кривизны профилей зубьев в точке контакта (К) равны расстоянию от этой точки до точки касания основной окружности N₁ и N₂ (по свойству эвольвенты), выражения для определения коэффициентов скольжения можно записать в следующем виде

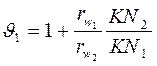
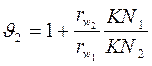
Подставив в полученные выражения граничные положения точки контакта (N₁,W и N₂ ), можно увидеть (см. рисунок) что, коэффициент скольжения изменяется от +1 у вершины зуба до -∞ -у ножки зуба, проходя через 0 в полюсе зацепления. Но так, как точка контакта при вращении колёс перемещается на линии зацепления от точки а₂, до точки а₁, то коэффициент скольжения у ножки зуба имеет конечное значение (см. на рисунке заштрихованную зону), хотя, как правило, большее, чем при вершине зуба. В полюсе зацепления скольжение отсутствует (чистое перекатывание).

С учетом того, что зуб колеса участвует в зацеплении меньшее число раз, чем зуб шестерни, целесообразно сопоставлять величины 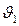и 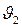через u₁₂. Это имеет особое значение при большихпередаточных отношениях.

Дата добавления: 2014-01-04