Цены котируемых деривативов

Любое решение дифферециального уравнения (14.16) 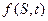является теоретической ценой некого возможного дериватива. Если дериватив с такой ценой существует, арбитражные возможности создать невозможно. И, наоборот, если функция 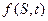не удовлетворяет дифференциальному уравнению (14.16), она не может быть ценой никакого дериватива без дополнительного создания арбитражных возможностей.

Чтобы проиллюстрировать это утверждение, рассмотрим функцию e^S. Она не является решением уравнения (14.16). Следовательно, ее нельзя считать ценой дериватива, зависящего от цены акции. Если на рынке постоянно существует производная ценная бумага с ценой e^S, могут возникнуть арбитражные возможности. В качестве второго примера рассмотрим функцию:

Она удовлетворяет дифференциальному уравнению (14.16) и поэтому, теоретически, является ценой некого дериватива. Она представляет собой цену дериватива, доходность которого в момент Т равна 1/S_T.

Дата добавления: 2014-01-04