Американские опционы

Перейдем к анализу американского опциона. В лекции 9 показано, что при отсутствии дивидендов американский опцион никогда не следует исполнять досрочно. Если же дивиденды выплачиваются, то досрочное исполнение опциона является оптимальным только непосредственно перед наступлением даты «без дивиденда». Предположим, что на протяжении срока действия опционов ожидается n дат «без дивиденда», а 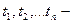моменты, непосредственно предшествующие этим датам, причем Дивиденды, соответствующие этим датам, будем обозначать символами D₁, D₂, …, D_n соответственно.

Оценим вариант досрочного исполнения опциона непосредственно перед наступлением последней даты «без дивиденда» (т.е. в момент t_n). Если инвестор исполняет опцион в этот момент, сумма, которую он получит, равна:

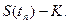
Если опцион не исполняется, цена акции падает до величины S(t_n) – D_n. Как следует из формулы (9.23), в этом случае стоимость опциона больше, чем:

Отсюда следует, что если

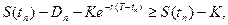
т.е.

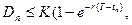(14.24)

то исполнение опциона не является оптимальным решением. Если же:

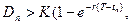(14.25)

То при любом достаточно естественном предположении о стохастическом процессе, описывающем поведение цены акции, можно показать, что досрочное исполнение опциона в момент t_n является оптимальным, если S(t_n) является достаточно большой. Неравенство (14.25), как правило, выполняется тогда, когда сроки выплат дивидендов очень близки к моменту завершения опциона (т.е. разница между T-t_n мала), а сумма дивиденда велика.

Перейдем к моменту досрочного исполнения опциона непосредственно перед наступлением предпоследней даты «без дивиденда» (т.е. в момент t_n-1). Если инвестор исполняет опцион в этот момент, сумма, которую он получит, равна:

Если опцион не исполняется, цена акции падает до величины S(t_n-1) – D_n-1, и ближайшая выплата дивидендов состоится в момент t_n. Как следует из формулы (9.23), нижняя граница стоимости опциона, не исполняемого в момент t_n равна:

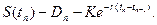
Отсюда следует, что если:

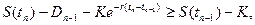
т.е.

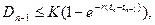
то исполнение опциона в момент t_n-1 не является оптимальным решением. Аналогично для любого i<n, если

(14.26)

то исполнение опциона в момент t_i нецелесообразно.

Неравенство (14.26) приближенно эквивалентно неравенству

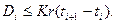
Если величина К почти совпадает с текущей ценой акции, то для выполнения этого неравенства необходимо, чтобы размер дивиденда либо почти совпадал, либо превышал безрисковую процентную ставку. Это условие выполняется довольно редко.

Итак, анализ показал, что в большинстве ситуаций единственный момент времени, который подходит для досрочного исполнения американского опциона «колл», - момент t_n, предшествующий последней выплате дивидендов. Более того, если неравенства (14.26) для всех i=1,2, …, n-1 и (14.24) выполняется одновременно, то досрочное исполнение американского опциона «колл» никогда не является оптимальным.

Дата добавления: 2014-01-04