Пример 14.9

Аппроксимация Блэка

Блэк предложил процедуру аппроксимации, позволяющую учесть досрочное исполнение опционов «колл». На первом этапе этой вычислительной процедуры вычисляется стоимость двух европейских опционов, сроки действия которых истекают в моменты Т и t_n. На втором этапе стоимость американского опциона приравнивается к стоимости более дорогого европейского опциона. Доказано, что в большинстве случаев эта аппроксимация работает хорошо.

Рассмотрим ситуацию, описанную в примере 14.8, но теперь будем считать, что опцион является не европейским, а американским. Кроме того, предположим, что D₁ = D₂ = 0,5; S₀ = 40, K = 40, r=0,09, t₁ = 2/12, t₂ = 5/12. Поскольку число

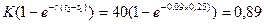
больше 0,5, то из неравенства (14.35) следует, что если этот опцион приносит большую прибыль, его следует исполнить непосредственно перед наступлением второй даты «без дивиденда».

Применим для вычисления стоимости опциона аппроксимацию Блэка. Текущая стоимость первого дивиденда равна:

Поэтому стоимость опциона, исполняемого непосредственно перед наступлением даты его окончания, можно вычислить по формуле Б-Ш при S₀ = 40 -0,4926 = 39,5074, K = 40, r = 0,09, σ = 0,30, T = 0,4167. Она равна 3,52 долл. В соответствии с процедурой аппроксимации Блэка, мы должны сравнить стоимость этого опциона со стоимостью опциона, который исполняется только по истечении шести месяцев. Из примера 12.8 мы знаем, что она равна 3,67 долл. Выбирая бóльшую из этих величин, получаем, что стоимость американского опциона «колл» равна 3,67 долл.

& Литература: монографии

1. Адельмейер М. Опционы колл и пут. М. 2004.
2. Балабушкин А. Н. Опционы и фьючерсы. М 1996.
3. Буренин А.Н. Задачи с решениями по рынку ценных бумаг, срочному рынку и риск-менеджменту. М. 2006.
4. Буренин А.Н. Рынки производных финансовых инструментов. М. 1996.
5. Буренин А.Н. Рынок ценных бумаг и производных финансовых инструментов. М. 1998.
6. Буренин А.Н. Фьючерсные, форвардные и опционные рынки. М. 1995.
7. Буренин А.Н. Форварды, фьючерсы, опционы, экзотические и погодные производные. М. 2005.
8. Вейсвеллер Р. Арбитраж. М. 1995.
9. Галанов В.А. Производные инструменты срочного рынка. М. 2002.
10. Де Ковни Ш., Таки К. Стратегия хеджирования. М. 1996.
11. Ибрагимова Л.Ф. Рынки срочных сделок. М. 1999.
12. Иванов К. Фьючерсы и опционы (механизм сделок). М. 1993.
13. Колб Р.У. Финансовые деривативы. М. 1997.
14. Криничанский К. В. Рынок ценных бумаг. М. 2007.
15. Макмиллан Л. Г. Опционы как стратегическое инвестирование. М. 2003.
16. Михайлов Д. М. Современные долговые и финансовые производные инструменты мирового рынка ссудных капиталов. М. 1998.
17. Рубцов Б. Б. Современные фондовые рынки. М. 2007.
18. Салыч Г. Г. Опционные, фьючерсные и форвардные контракты: сверхприбыльные инвестиции в период инфляции. М. 1994.
19. Сафронова Т.Ю. Биржевая торговля производными инструментами. М. 2000.
20. Томсетт М. Торговля опционами. М. 2001.
21. Фельдман А. Б. Основы рынка производных ценных бумаг. М. 1996.
22. Фельдман А.Б. Производные финансовые и товарные инструменты. М. 2003.
23. Халл Дж. К. Опционы, фьючерсы и другие производные финансовые инструменты. 6-е изд. М. 2007.
24. Чесноков А. С. Инвестиционная стратегия, опционы и фьючерсы. М. 1993.
25. Чикагская торговая палата. Коммерческая стратегия. М. 1993.
26. Шарп У.Ф., Александер Г. Дж. Бэйли Дж. В. Инвестиции. М. 1999.
27. Шварц Ф. Биржевая деятельность Запада: фьючерсные и фондовые биржи, система работы и алгоритм анализа. М. 1992.

[1] См.: Black F., Scholes M. The Pricing of Options and Corporate Liabilities //Journal Political Economy, 81 (May/June 1973). P. 637-659: Merton R.C/ Theory of Rational Option Pricing //Bell Journal of Economics and Management Science. 4 (Spring 1973). P. 141-183.

[2] Финансовая инженерия – проектирование, разработка и реализация инновационных финансовых инструментов и процессов, а также творческий поиск новых подходов к решению проблем в области финансов.

[3] Итак, мы показали, что термин «ожидаемая доходность» является неоднозначным. Он может относиться как к величине µ - σ²/2, так и к величине µ. Если не указано иное, в дальнейшем на протяжении всего курса термин «ожидаемая доходность» будет относиться к величине µ.

[4] Этот метод описан только для иллюстрации. На практике такие уравнения решаются с помощью более мощных методов, например, метода Ньютона-Рафсона. Для вычисления подразумеваемой волатильности можно также применять программу DerivaGem.

[5] С учетом налогов цена акции может уменьшиться на величину, немного превышающую сумму наличного дивиденда. Чтобы учесть это явление, при оценке опционов слово «дивиденд» следует интерпретировать в зависимости от контекста. Например, если дивиденд равен одному доллару и цена акции в момент его выплаты снижается на 80% его размера, то для дальнейшего анализа следует предположить, что величина дивиденда равна 0,8 долл.

[6] С теоретической точки зрения эта волатильность не эквивалентна изменчивости стохастического процесса, описывающего поведение цены акции. Волатильность рискованного компонента приближенно равна волатильности цены акции, умноженной на коэффициент S₀/(S₀ – D), где D – текущая стоимость дивидендов. Однако поправка необходима лишь тогда, когда волатильность оценивается по ретроспективным данным. Изменчивость рискованного компонента эквивалентна подразумеваемой волатильности, которая вычисляется по данным, полученным после вычета из цены акции текущей стоимости дивидендов.

Дата добавления: 2014-01-04