Прямоугольное окно

Весовые множители в методе Фурье-преобразований.

Последствия "усечения" импульсной характеристики равнозначны эффекту введения в уравнение фильтра дополнительных весовых множителей ω_k.

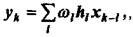(1)

где

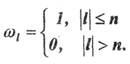(2)

В результате вместо оптимальной импульсной характеристики h_k используется конечная импульсная характеристика ω_k h_k.

Вычислим частотную характеристику фильтра (1):

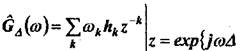(3)

Обозначим W_z(z) и H(z) Z-преобразования последовательностей ω_k и h_k, тогда из свойств Z-преобразования следует, что

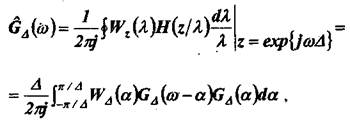(4)

где

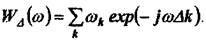(5)

Функцию (5) называют "частотным окном просмотра данных" (в отличие от временного "окна", то есть набора весовых коэффициентов (2)). Выбор весовых множителей, разумеется, не является единственным. Последовательность ω_k, определенную выше называют прямоугольным окном. Свойства тех или иных окон просмотра данных часто формулируют в терминах свойств функции W_Δ(ω). Для прямоугольного окна получаем (см. рис.1):

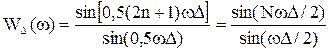(6)

Для того чтобы понять, каким образом свойства функции (6) влияют на характеристики фильтра, удобно разложить W_Δ(ω) на два слагаемых:

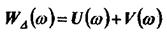(7)

где

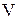
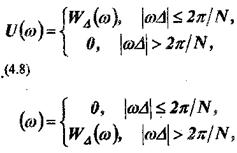(8,9)

тогда

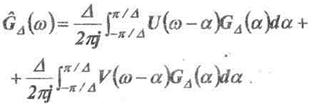(10)

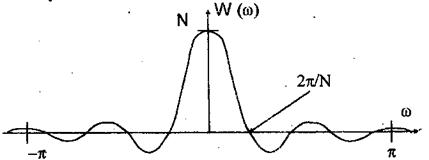
Рис.1. Частотная характеристика прямоугольного окна.

Из (10)(п.л.) следует, что введение весовых множителей искажают G_Δ(ω) в силу воздействия следующих двух факторов (см. рис.2):

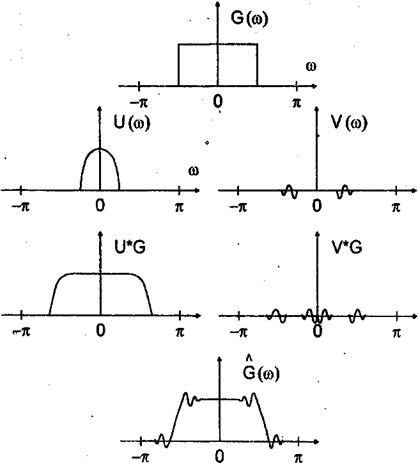
Рис.4.2. Графическая иллюстрация свертки функций G(ω) и W(ω) (см.(10))

а) влияние "центрального лепестка" (то есть функции U(ω)), которое сводится к размыванию полос пропускания и непропускания и объясняет уменьшение крутизны амплитудных характеристик;

б) влияние "боковых лепестков" (функции V(ω))> приводящее к появлению пульсаций и выбросов (явление Гиббса).

Дата добавления: 2014-01-04