Тензор инерции

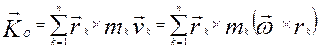
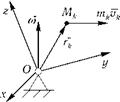Рассмотрим выражение кинетического момента твердого тела в случае его сферического движения. С учетом формулы Эйлера для скорости точки име­ем

где 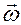— мгновенная угловая скорость сферического движения.

В проекциях на оси системы координат, связанной с движущимся те­лом,

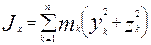
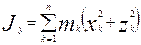
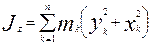- осевые моменты инерции

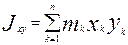
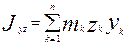
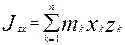- центробежные моменты инерции (= , = , = )

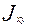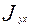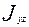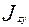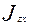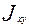В фиксированном базисе 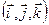матрица

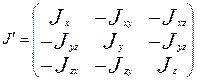- тензор инерции.

Матрица J является симметричной и ее элементы определяются мо­ментами инерции твердого тела, характеризующими распределение масс относительно фиксированной системы координат.

Как известно, при изменении базиса (преобразовании системы коорди­нат) матрицу линейного преобразования можно привести к диагональному виду

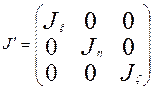соответствующие оси ,,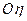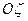- главные оси инерции твердого тела. Если начало координат совпадает с центром масс, то они называются главными центральными осями инерции. Главной осью инерции, кроме того, по определению называется ось координат, для которой центробежные моменты инерции содержащие индекс этой оси, равны нулю.

Моменты инерции некоторых однородных тел, моделируемых простей-

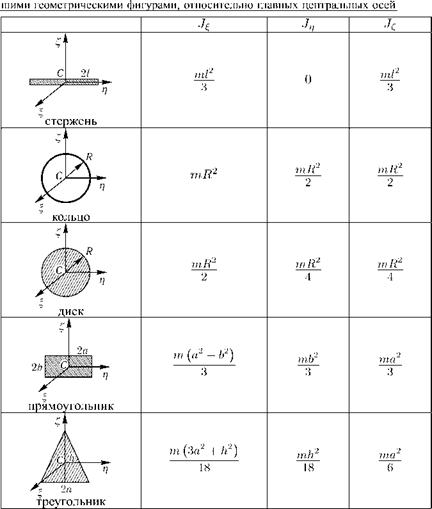
В частности, момент инерции относительно произвольной оси Ох, со-
ставляющей углы 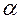, , 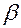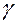с главными осям ,,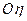, 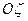в соответствии
с указанным правилом перехода от одного базиса к другому определится равенством

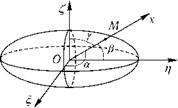
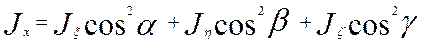
Теорема Гюйгенса - Штейнера. Момент инерции относительно про­извольной оси равен моменту инерции относительно параллельной оси, про­ходящей через центр масс, сложенному с произведением массы тела на квадрат расстояния между осями

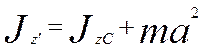
Где 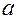- расстояние между осями.

Дата добавления: 2014-01-04