Динамические уравнения Эйлера

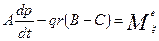
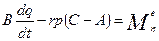
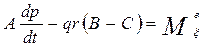
Эти уравнения называются динамическими уравнениями Эйлера. Они допускают аналитическое интегрирование при произвольных начальных условиях движения в трех случаях.

Случай Эйлера-Пуансо. Центр масс тела произвольной формы сов­падает с неподвижной точкой. Движение тела происходит по инерции.

Случай Лагранжа-Пуассона. Эллипсоидом инерции для непо­движной точки является эллипсоид вращения А = В 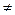С и центр масс лежит на оси вращения эллипсоида инерции. (Симметричный волчок.)

Случай Ковалевской. Эллипсоид инерции для неподвижной точки есть вытянутый эллипсоид вращения при А = В = 2С. Центр масс тела лежит в экваториальной плоскости эллипсоида инерции. (Асимметричный волчок.)

Дифференциальные уравнения свободного движения твердого тела

Дифференциальные уравнения свободного движения твердого тела нетрудно получить, если рассмотреть движение тела как сложное, принимая за переносное движение поступательное с центром масс, а за относитель­ное — сферическое движение вокруг центра масс. Т. е. к динамическим уравнениям Эйлера необходимо добавить дифференциальные уравнения движения центра масс.

Приближенная теория гироскопа

Гироскоп — быстро вращающееся симметричное твердое тело, ось вра­щения которого (ось симметрии) может изменять свое направление в про­странстве. Гироскопы обладают рядом интересных свойств, обусловливаю­щих их широкое применение в различных технических устройствах. В каче­стве примера на рисунке изображены гироскоп с тремя степенями свободы, когда ротор может совершать три независимых вращения вокруг осей АА В В', С С', пересекающихся в одной точке О (карданов подвес), и гироскоп с двумя степенями свободы, когда ротор может вращаться только вокруг осей АА', В В'.

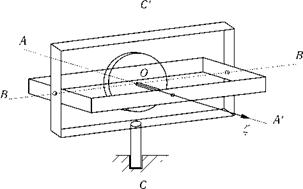
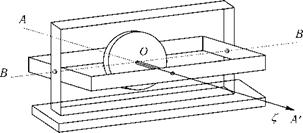
Гироскопы совершают сферическое движение. Если неподвижная точ­ка О совпадает с центром масс, то такой гироскоп называется астатическим (уравновешенным), в противном случае — тяжелым.

Элементарная или прецессионная теория гироскопа основана на допу­щении, что угловая скорость вращения гироскопа вокруг оси материальной симметрии значительно превышает угловую скорость поворота этой оси.

Пусть — угловая скорость быстро вращающегося гироскопа, С02 — угловая скорость вращения оси гироскопа. В рамках прецессионной теории можно считать, что кинетический момент гироскопа относительно непо­движной точки направлен вдоль оси симметрии гироскопа 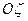и равен

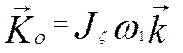
Теорема Резаля

Теорема. Скорость конца вектора кинетического момента механиче­ской системы относительно некоторого неподвижного центра геометри­чески равна главному моменту внешних сил, действующих на эту систему, относительно того же центра.

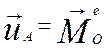
Используя теорему Резаля, можно:

Зная внешние силы, найти, как движется ось гироскопа.

Зная движение оси гироскопа, можно найти главный момент внеш­них сил.

Дата добавления: 2014-01-04