Уравнение колебательного контура

ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ

Электрические колебания возникают в цепи при изменении тока в ней и в каждый момент времени ток неодинаков на различных участках цепи, из-за конечности скорости распространения электромагнитных волн. Если же мгновенные значения тока на всех участках цепи практически одинаковы, то такой ток называют квазистационарным. При этом все изменения во времени должны происходить столь медленно, чтобы распространение электромагнитных возмущений можно было считать мгновенными.

Для периодически изменяющихся токов условие квазистационарности записывают в виде t = l/c << Т, где с - скорость света; Т - период колебаний тока; - длина электрической цепи. Для цепи длиной l= 3 м время t = 10^-8 с, поэтому токи можно считать квазистационарными вплоть до частот колебаний n = 10⁶ Гц, т. е. Т = 10^-6 с. В этом случае мгновенные значения токов подчиняются закону Ома.

Рассмотрим электрическую цепь, содержащую конденсатор емкости С и катушку индуктивности L, в которой возникают электрические колебания. Такую систему называют колебательным контуром с сосредоточенными параметрами (рис. 8.1).

После зарядки конденсатора вся энергия колебательного контура сосредоточена в конденсаторе (энергия электрического поля, рис. 8.1, а).

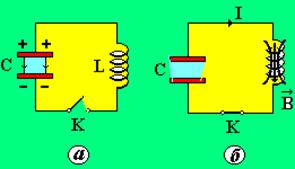Рис. 8.1

При разряде конденсатора через катушку индуктивности потечет ток и в ней возникнет переменное магнитное поле.

При полном разряде конденсатора ток в цепи достигнет максимума (рис. 8.1, б).

Энергия переменного электрического поля перешла в энергию переменного магнитного поля.

С этого момента ток, не меняя направления, начнет убывать.

Но он прекратится не сразу, т. к. ЭДС самоиндукции, индуцирует в цепи индукционный ток, того же направления.

Ток будет перезаряжать конденсатор, и возникшее электрическое поле будет ослаблять его. Когда ток прекратится, перезарядка конденсатора полностью закончится.

С этого момента конденсатор будет разряжаться и т. д. - процесс будет повторяться.

В колебательном контуре при отсутствии сопротивления проводников будут совершаться строго периодические электрические колебания.

При этом на обкладках конденсатора будет периодически изменяться заряд, напряжение на нем и ток через катушку индуктивности.

Если сопротивление проводников R ¹ 0, то часть электромагнитной энергии будет превращаться в теплоту Джоуля-Ленца и в конце концов электрические колебания в контуре прекратятся.

Для их поддержания необходимо периодически пополнять энергию в контуре от стороннего источника тока.

Найдем уравнение колебаний в контуре, содержащем внешнюю ЭДС, активное сопротивление R, индуктивность L и емкость С (рис. 8.2).

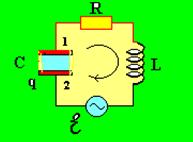  Рис. 8.2

Ток в колебательном контуре

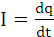. (8.1)

Если I > 0, то и dq > 0.

Применим закон Ома для неоднородного участка цепи 1RL2:

IR = j₁ - j₂ + _S + , (8.2)

где _S = - ЭДС самоиндукции; (j₁ - j₂)- разность потенциалов на обкладках конденсатора (если q > 0, то j₁ - j₂ < 0, так как С > 0).

Дата добавления: 2014-01-04