
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вычисление линейного интеграла
|
|
|
|
Современные принципы профилактики и борьбы с гельминтозами.
Основные принципы профилактики и борьбы с гельминтозами.
Основные принципы сформулировал Скрябин. Для профилактики гельминтозов в 1925 году он предложил принцип дегельминтизации, который основан на сочетании терапии и профилактики. Он предусматривает освобождение человека и животных от гельминтов с помощью медикаментов и последующее уничтожение выделенных паразитов и их расселительных стадий средствами дезинфекции. Эта мера примитивная, т.к. не приводит к уничтожению гельминта как вида.
В 1944 году был предложен принцип девастации, который предполагает уничтожение гельминтов как биологических видов во всех средах их обитания на всех стадиях жизненного цикла всеми возможными средствами и методами.
1. Комплекс мер, направленных на источник инвазии (активное выявление и дегельминтизация инвазированных – проведение обследования декретированных контингентов (работники пищеблоков, детских учреждений, группы риска), выборочное обследование в очагах инвазий.
2. Меры, направленные на факторы передачи, охрана внешней среды от загрязнений яйцами или личинками гельминтов, ее обеззараживание (благоустройство населенных мест в соответствии с санитарными требованиями, обеззараживание сточных вод, борьба с грызунами, правильное содержание и выгул животных).
3. Ветеринарный надзор на убойных пунктах, повышение санитарной грамотности населения, санитарно-просветительная работа.
Не доказывая, сформулируем правило вычисления линейных интегралов 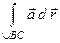 в следующих двух случаях.
в следующих двух случаях.
1). Для вычисления интеграла 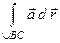 по линии
по линии 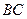 , заданной уравнениями
, заданной уравнениями 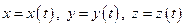 , следует:
, следует:
а) записать интеграл в координатной форме
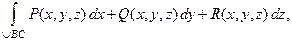
б) заменить 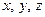 в функциях
в функциях 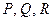 соответственно на
соответственно на 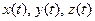 ,
,
в) заменить 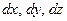 соответственно на
соответственно на 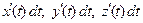 ,
,
г) найти интервал изменения параметра 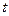 и вычислить получившийся определенный интеграл по этому интервалу.
и вычислить получившийся определенный интеграл по этому интервалу.
2). Для вычисления интеграла 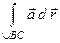 по плоской линии
по плоской линии 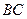 с уравнением
с уравнением 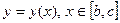 следует:
следует:
а) записать интеграл в координатной форме 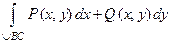 ,
,
б) заменить  в функциях
в функциях  на
на 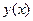 ,
,
в) заменить 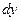 на
на 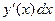 ,
,
г) вычислить получившийся определенный интеграл по отрезку 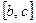 .
.
3). В случае центрального поля 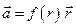 следует учесть, что
следует учесть, что 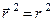 ; дифференцируя это равенство, получим
; дифференцируя это равенство, получим 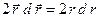 и
и
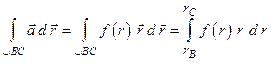 ,
,
т.е. линейный интеграл поля сведен к определенному интегралу.
Пример 11.1. Вычислить работу силы 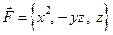 по прямолинейному перемещению из точки
по прямолинейному перемещению из точки 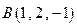 в точку
в точку 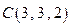 .
.
Решение. Работа 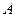 силы
силы 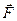 вычисляется по формуле
вычисляется по формуле
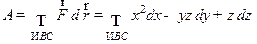 .
.
Для вычисления этого интеграла составим уравнение прямой 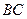 :
:
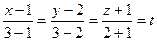 .
.
Отсюда 
Найдем значение параметра 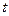 , соответствующее точке
, соответствующее точке 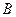 . Для этого подставим абсциссу
. Для этого подставим абсциссу 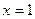 точки
точки 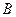 в формулу
в формулу  . Получим
. Получим  . Аналогично найдем
. Аналогично найдем 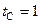 . Заменяя в интеграле
. Заменяя в интеграле 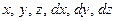 их выражениями, получим
их выражениями, получим
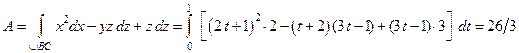 .
.
 Пример 11.2. Найти циркуляцию поля
Пример 11.2. Найти циркуляцию поля  вдоль линии
вдоль линии 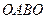 , где
, где 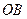 ─ дуга параболы
─ дуга параболы 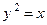 ,
,  ─ ломаная (рис. 67).
─ ломаная (рис. 67).
Решение. Циркуляцию поля  вычислим по формуле
вычислим по формуле
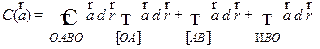 .
.
На отрезке 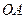 имеем
имеем 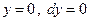 . Поэтому
. Поэтому
|
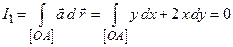 .
.
На отрезке 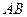 имеем
имеем 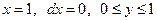 . Поэтому
. Поэтому
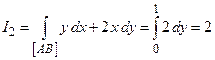 .
.
На дуге  имеем
имеем 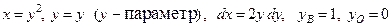 . Поэтому
. Поэтому
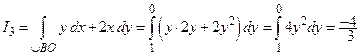 .
.
Окончательно,  .
.
Пример 11.3. Вычислить циркуляцию поля 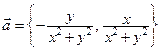 по окружности
по окружности  радиусом
радиусом  с центром в начале координат, ориентированной против часовой стрелки.
с центром в начале координат, ориентированной против часовой стрелки.
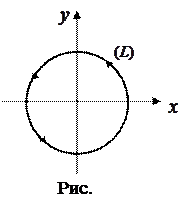 Решение. Циркуляция поля
Решение. Циркуляция поля  вычисляется по формуле
вычисляется по формуле

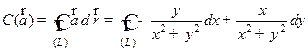 .
.
|
 Для вычисления этого интеграла запишем параметрические уравнения окружности
Для вычисления этого интеграла запишем параметрические уравнения окружности  :
:  .
.
|
 ,
,  ; угол
; угол  при движении против часовой стрелки меняется от
при движении против часовой стрелки меняется от  до
до  (рис. 68). Поэтому
(рис. 68). Поэтому 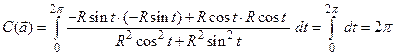 .
.|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1146; Нарушение авторских прав?; Мы поможем в написании вашей работы!