Формулы Грина и Стокса. Ротор поля

Циркуляцию, как линейный интеграл поля по замкнутому контуру, можно вычислять способами, изложенными в п. 11.3. Однако часто удобно вычислять циркуляцию плоского поля по формуле Грина, а циркуляцию пространственного поля

─ по формуле Стокса.

Если при обходе замкнутого контура ограниченная область остается слева,

то направление обхода называют положительным. Обход в противоположном направлении называют отрицательным.

Теорема 11.1. Пусть функции 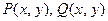и их частные производные непрерывны в области с положительно ориентированной границей . Тогда имеет место следующая формула Грина:

. (11.5)

Доказательство проведем для области , описываемой неравенствами (рис. 69).

Сначала проверим равенство

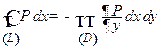. (11.6)

Сведем криволинейный интеграл 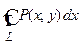к определенному интегралу, подставляя на лини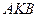и и на линии :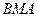

Теперь преобразуем двойной интеграл, сведя его сначала к повторному, а затем к определенному интегралу:

.

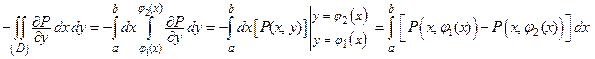И криволинейный, и двойной интегралы из формулы (11.6) равны одному и тому же определенному интегралу и, следовательно, равны между собой. Аналогично проверяется равенство

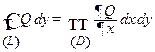. (11.7)

Складывая равенства (11.6) и (11.7), получим формулу Грина.

Замечание. Нарушение условий теоремы Грина может привести к неверным результатам. Например, для поля нетрудно проверить, что

,

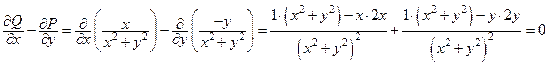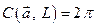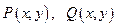но циркуляция поля по окружности с центром в начале координат отличнаот нуля, (пример 11.3). В этом примере нарушены условия теоремы Грина, т.к. внутри контура содержится точка , в которой функции не определены.

Пример 11.4. Используя формулу Грина, вычислить циркуляцию поля вдоль линии 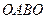(рис. 67).

Решение. Вычислим циркуляцию 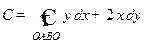, используя формулу Грина для : .

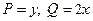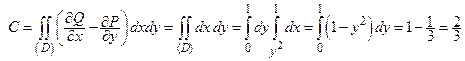Сравните это решение с решением примера 11.2, где циркуляция этого поля была вычислена без формулы Грина.

Для обобщения формулы Грина на пространственный случай введем понятие ротора векторного поля .

Ротором векторного поля 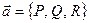называется вектор

. (11.8)

При вычислении следует разложить определитель по элементам первой строки. Учитывая, что 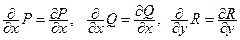и т. д., получим

.

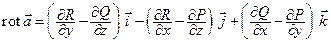Понятие ротора позволяет удобно вычислять циркуляцию векторного поля, опираясь на следующую теорему (доказательство теоремы опустим).

Теорема 11.2. Пусть функции и их частные производные непрерывны на ориентированной поверхности , натянутой на контур , причем ориентации контура и поверхности 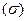согласованы. Тогда имеет место следующая формула Стокса:

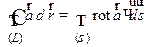. (11.9)

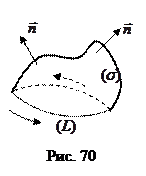В этой формуле ориентации контура и поверхности 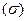согласованы, т. е., глядя с конца выбранных нормальных векторов поверхности 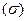, обход контура виден против часовой стрелки (рис. 70).

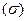Итак, по формуле Стокса циркуляция поля по контуру равна потоку ротора поля через поверхность , натянутую на контур .

Пример 11.5. Для поля найти его циркуляцию по окружности , лежащей в плоскости и ориентированной против часовой стрелки, если смотреть с конца оси 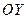(рис. 71).

Решение. Циркуляция поля вычисляется по формуле 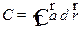. Непосредственное вычисление этого интеграла достаточно трудоемко. Посмотрим, облегчит ли вычисление циркуляции применение формулы Стокса. Для этого вычислим ротор

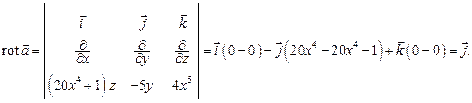
По формуле Стокса имеем:

.

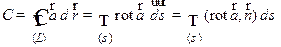В качестве поверхности 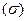, натянутой на окружность, возьмем круг, ограниченный этой окружностью. Нормальный вектор к этой поверхности направлен вдоль оси 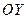, т.е. 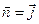; скалярное произведение ;

.

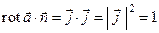Остановимся более подробно на свойствах ротора.

Дата добавления: 2014-01-04