Физический смысл ротора

Пусть твердое тело вращается с постоянной угловой скоростью 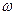. Найдем поле линейных скоростей точек тела и ротор этого поля.

Рассмотрим систему координат, направив ось 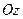по оси вращения (рис. 72). Как известно из кинематики, линейная скорость 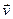точки 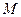равна векторному произведению 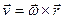, где 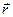─ радиус-вектор точки 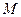, , 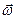─ вектор угловой скорости, направленный по оси вращения с длиной, равной величине угловой скорости 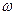, т. е. .

Найдем поле линейных скоростей:

Рис. 73

Рис. 72

.

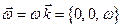Ротор этого поля вычислим по формуле (11.8):

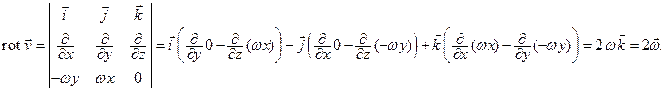Таким образом, ротор поля линейных скоростей в любой точке равен удвоенному вектору угловой скорости.

В произвольном поле его ротор, вычисленный в точке 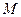, также характеризует вращательную способность поля в этой точке.

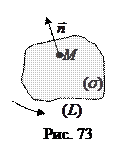Инвариантное определение ротора

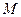Рассмотрим некоторую поверхность , содержащую точку , и единичный нормальный вектор 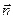этой поверхности (рис. 73). Вычислим по формуле Стокса циркуляцию поля по произвольному контуру , лежащему на поверхности :

.

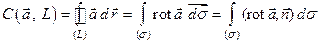Воспользуемся теоремой о среднем для поверхностного интеграла 1-го рода:

.

Переходя в последнем равенстве к пределу при стягивании поверхности в точку 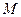, получим:

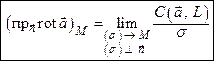. (11.10)

Эту величину называют плотностью циркуляции поля 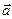в точке 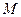в направлении вектора 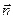. Плотность циркуляции, как проекция 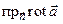, принимает наибольшее значение, равное , когда векторы и 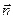сонаправлены. Поэтому получаем следующее инвариантное (не зависящее от системы координат) определение ротора.

Ротор поля 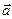в точке 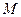есть вектор, удовлетворяющий условиям:

а) в направлении этого вектора плотность циркуляции поля 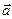в точке 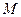принимает наибольшее значение,

б) по величине он равен наибольшей плотности циркуляции поля 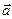в точке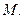

Дата добавления: 2014-01-04