ЛЕКЦИЯ 17. Сложное сопротивление стержней. Косой изгиб. Изгиб с кручением. Расчёты на прочность и жёсткость

Под сложным сопротивлением понимается такой вид деформации, при котором брус испытывает не одну, а несколько простых деформаций (осевое растяжение-сжатие, кручение, прямой поперечный изгиб). Из множества видов сложного сопротивления выделяют три основных: растяжение (сжатие) с изгибом, косой изгиб, изгиб с кручением.

При сложном сопротивлении могут возникать несколько внутренних усилий, в наиболее общем случае все шесть (лекция 2): N, Q_y, Q_z, M_x, M_y, M_z. Правило знаков для продольной и поперечной сил, а также крутящего момента прежние, а изгибающий момент будет положителен, если вызывает растягивающие напряжения в волокнах, расположенных в первой четверти координат. При рассмотрении случаев сложного сопротивления оси z и y будем совмещать с главными центральными осями инерции.

Рассмотрим относительно простой случай нагружения бруса (рис.17.1).

Рис. 17.1. Сложный вид сопротивления (слева) и внутренние усилия, соответствующие ему (справа)

В данном случае N = 0, Q_y= F, Q_z = 0, M_x = F(b/2), M_y = 0, M_z = F(l - x). Таким образом, балка испытывает изгиб и кручение.

В простых видах сопротивления для определения напряжений использовались следующие формулы. Осевое растяжение (сжатие):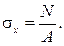

Кручение круглого стержня:

Поперечный изгиб в плоскости Оxy:

Поперечный изгиб в плоскости Оxz: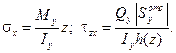

Используя принцип суперпозиции или принцип независимости действия сил, получим формулу нормальных напряжений: 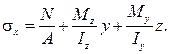(17.1)

Для получения зависимости для касательных напряжений рассмотрим рис. 17.2.

Рис. 17.2. Касательные напряжения в точке А круглого сечения при изгибе с кручением

Полное касательное напряжение вблизи точки А может быть вычислено с помощью геометрического суммирования:

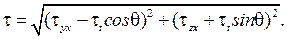(17.2)

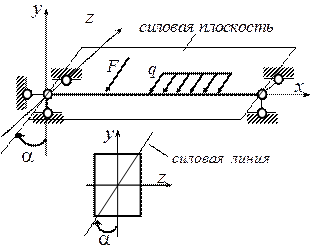
Косой изгиб – изгиб, при котором плоскость действия суммарного изгибающего момента в сечении балки не совпадает ни с одной из главных плоскостей инерции. Различают два вида косого изгиба: плоский и пространственный (рис 17.3). При плоском косом изгибе внешние силы действуют в одной плоскости, не совпадающей с главными плоскостями инерции. Эта плоскость называется силовой, а линия её пересечения с поперечным сечением балки – силовой линией. При пространственном косом изгибе внешние силы действуют в различных плоскостях.

Рис. 17.3. Плоский (справа) и пространственный (слева) косой изгиб

Обозначим угол между силовой линией и главной осью y через α. Суммарный изгибающий момент, возникающий в сечении балки (рис. 17.3) можно разложить на два изгибающих момента М_z и М_y, соответствующих главным плоскостям инерции:

(17.3)

Поделим первое из этих равенств на второе, выразим угол α через отношение изгибающих моментов

(17.4)

При пространственном изгибе величина угла α изменяется по длине балки.

Рис. 17.4. Пространственный косой изгиб (слева) внутренние усилия и эпюра напряжений, соответствующие такой деформации

Для определения напряжений при косом изгибе можно использовать зависимость (17.1), которая запишется как

(17.5)

Здесь I_z и I_y – главные моменты инерции сечения, z, y – координаты точек сечения.

Из зависимости (17.5) видно, что напряжение изменяется по линейному закону.

Найдём координаты нулевой линии, т.к. на нейтральной оси напряжение равно нулю, то получим

(17.6)

где z₀, y₀ – координаты нейтральной оси.

Обозначим через φ угол между нейтральной осью и осью z и найдём из (17.6):

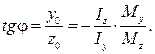
Учитывая (17.4) получим соотношение, связывающее между собой углы φ и α.

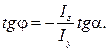(17.8)

Знак «-» в этой зависимости указывает на то, что нулевая линия по отношению к силовой проходит через две другие четверти.

Для сечений типа прямоугольника или двутавра, имеющих две оси симметрии, наибольшие по абсолютной величине напряжения удобно вычислять по формуле

(17.9)

А в случае произвольного сечения лучше воспользоваться зависимостью

(17.10)

Тогда условия прочности при косом изгибе запишутся как

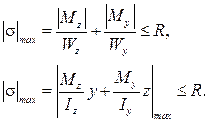(17.11)

В нижней формуле М_z, М_y, z, y необходимо брать с учётом знака.

Условия жёсткости. При косом изгибе возникают углы поворотов и прогибы (рис. 17.5). Используя принцип суперпозиции, отдельно определяют перемещения в разных плоскостях.

(17.12)

(17.13)

Рис. 17.5. Перемещения при косом изгибе

Изгиб с кручением. При изгибе с кручением возникают внутренние усилия Q_y, Q_z, M_t = M_x, M_y, M_z.

Изгиб с кручением стержней с круглым или трубчатым поперечным сечением. В данном случае удобно воспользоваться полным изгибающим моментом и свести расчёт к прямому изгибу.

(17.14)

В круглых или трубчатых сечениях нейтральная ось перпендикулярна следу плоскости результирующего момента (17.8), т. к. .

Рис. 17.6. Эпюры напряжений при изгибе с кручением

Касательным напряжением изгиба в силу малости пренебрегают, тогда нормальное и касательное напряжения можно найти как

(17.15)

здесь

На основе третьей и четвёртой теорий прочности можно записать

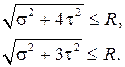(17.16)

С помощью этих условий можно решать все три типа задач.

Изгиб с кручением стержней прямоугольного поперечного сечения. Построим эпюры нормальных и касательных напряжений в прямоугольном поперечном сечении.

эп. σ (M_z) эп. τ (Q_y) эп. τ (M_t)

эп. σ (M_y)

эп. τ (Q_z)

Условие прочности по максимальным нормальным напряжениям (17.9).

Касательные напряжения можно определить как 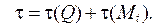Также используют условие прочности (17.16) по третьей теории прочности.

Расчёт на жёсткость производят отдельно для изгиба (17.12), (17.13) и для кручения (17.17).

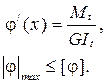(17.17)

Подробно определение перемещений при кручении рассмотрено в лекциях 10 и 11.

Дата добавления: 2014-01-04