Функция готовности и коэффициент готовности

Показатели надежности восстанавливаемых систем

ОСОБЕННОСТИ РЕЗЕРВИРОВАННЫХ ВОССТАНАВЛИВАЕМЫХ СИСТЕМ

Восстанавливаемые в процессе эксплуатации системы можно разделить на две группы.

К первой группе относятся системы, для которых на протяжении заданной продолжительности работы допускаются отказы и вызванные ими кратковременные перерывы в работе. Для систем этой группы большое значение имеет свойство готовности, то есть способности находиться в процессе эксплуатации максимальное время в работоспособном и готовом к использованию состоянии.

Ко второй группе относятся системы, отказы которых в течение заданного времени недопустимы. Отказавшие элементы таких систем восстанавливаются в процессе работы системы. Например, при отказе элементов основной системы работает резервная система, а основная система в это время восстанавливается (ремонтируется).

Одна и та же система может быть отнесена к любой из этих групп в зависимости от режима ее эксплуатации.

Основными показателями надежности систем первой группы являются:

- функция готовности Г(t) - вероятность застать систему работоспособной в момент времени t:

- коэффициент готовности k_г — вероятность того, что система окажется работоспособной в любой момент времени, кроме периодов, в течение которых ее использование по назначению не предусмотрено (то есть отношение времени, в течение которого система работать способна, к общему времени ее работы по назначению);

- математическое ожидание времени работы системы между отказами и времени восстановления системы.

К основным показателям надежности систем второй группы относятся:

- условная вероятность безотказной работы на заданном интервале (0,t) при условии, что в начальный момент времени (до начала рассматриваемого интервала) все элементы системы работоспособны;

- параметр потока отказов ω*(t);

- математическое ожидание времени безотказной работы.

Рассмотрим некоторые показатели надежности первой и второй групп подробнее.

Определения функции готовности Г(t) и коэффициента готовности рассмотрим при допущении показательного закона распределения вероятностей времени между отказами и времени восстановления при постоянных значениях интенсивностей отказов (λ) и восстановления (μ).

Система будет работоспособной в момент времени (t + ∆t) при двух независимых событиях:

1) работоспособная до момента времени t система остается работоспособной на интервале времени (t,t+∆t);

неработоспособная (находящаяся на восстановлении) до момента времени t система восстановлена на протяжении времени (t,t+∆t).

Вероятность первого события

(5.47)

разложим экспоненту в (5.47) в ряд:

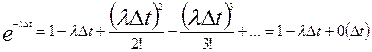
Здесь 0(∆t) - величина более высокого порядка малости, чем ∆t, с уменьшением ∆t она спадает быстрее, чем ∆t, так что

Тогда

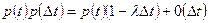(5.48)

Вероятность второго события равна произведению вероятности неисправного (неработоспособного) состояния системы до момента t на вероятность восстановления в течение времени (t,t+∆t):

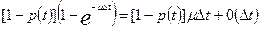(5.49)

где μ — вероятность восстановления работоспособности системы в единицу времени при условии, что до этого времени восстановления не произошло.

По теореме сложения вероятностей несовместных событий вероятность работоспособного состояния системы в момент времени (t+∆t) равна

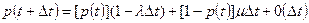(5.50)

Преобразуем (5.50) к виду

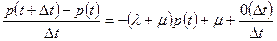
Устремляя ∆t к нулю, получим

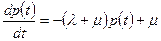(5.51)

или

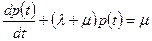(5.52)

Выражение (5.52) является линейным неоднородным дифференциальным уравнением первого порядка с постоянной правой частью. Его решение имеет вид

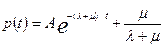(5.53)

Из условия р(t=0)=1 определяем величину постоянной интегрирования А=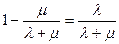. Тогда

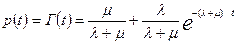(5.54)

Поскольку коэффициент готовности системы представляет собой отношение времени t работоспособного состояния системы к общему времени (t+t_в) использования системы по назначению (t_в — время восстановления системы после отказа), то

(5.55)

где M[t] и M[t_в] - математические ожидания случайных величин t и t_в

При стационарном режиме эксплуатации (t→∞)

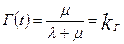(5.56)

Практически выражение (5.56) справедливо при t>10 ч. Например, при λ = 0,002 1/ч, μ = 0,2 ¹/ч, и t=5ч значение Г, вычисленное по (5.56), отличается от значения, вычисленного по (5.54), меньше чем на 0,4%.

Дата добавления: 2014-01-04