Лекция № 3, ВА-1, матан, 2 семестр

Тема. Интегралы, приводящиеся к интегралам «группы четырех» Интегрирование тригонометрических функций.

1. Некоторые интегралы, приводящиеся
к интегралам «группы четырёх»

К интегралам «группы четырех» путем тождественных преобразований и подходящей замены переменной сводятся многие интегралы, подынтегральная функция которых представляет дробь со знаменателем – квадратным трехчленом или квадратным корнем из него.

Рассмотрим интегралы вида 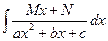и 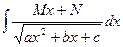, где М, N, a, b, c – заданные числа.

Для приведения этих интегралов к интегралам «группы четырёх» выделяем из квадратного трёхчлена полный квадрат, и выражение под знаком полного квадрата принимаем за новую переменную.

Покажем на конкретных примерах, как это делается.

Задача 1.1. Вычислить интеграл: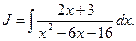

Решение. Данный интеграл имеет вид: ,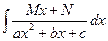

где 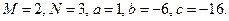Выделит полный квадрат в знаменателе подынтегрального выражения:

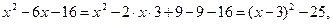
Полученным выражением заменим знаменатель данного интеграла и произведем замену переменной интегрирования

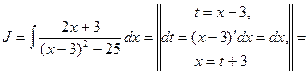
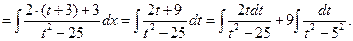
В последнем преобразовании мы воспользовались свойствами аддитивности и однородности неопределенных интегралов. Найдем каждый из интегралов в отдельности. Первый интеграл вычисляется с помощью очевидной подстановки, второй является табличным интегралом.

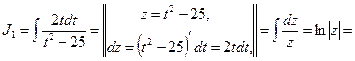
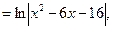
Обратим внимание на то, под знаком логарифма мы получили тот же трехчлен, что и под знаком корня в исходном интеграле. И это не случайно.

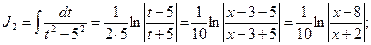
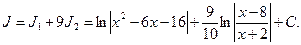
Задача 1.2. Вычислить интеграл: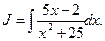

Решение. Интеграл имеет вид: 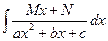, где 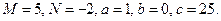Так как 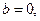то выделять полный квадрат не приходится. Тогда

;

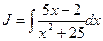
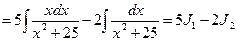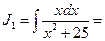
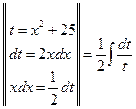
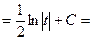
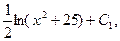=(см. формулу 4);

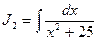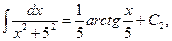=(см. формулу 11).

Окончательно получаем:

=.

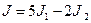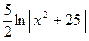
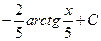Задача 1.3. Вычислить интеграл: .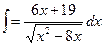

Решение. Интеграл имеет вид: 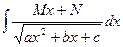, где

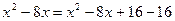
Тогда

==

;

;

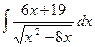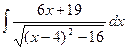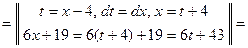
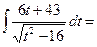
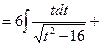
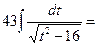
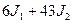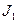
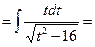
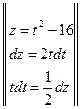
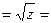
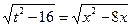по формуле 13:

;

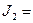
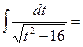
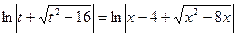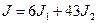
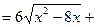
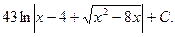
Задача 1.4. Вычислить интеграл: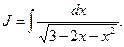

Решение. Интеграл имеет вид: 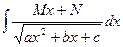, где 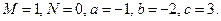Выделим полный квадрат в подкоренном выражении:

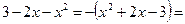
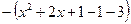
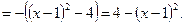
Заменим полученным выражением подкоренную функцию данного интеграла и проведем вычисления:

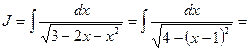
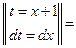
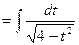
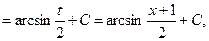(формула 10).

Задача 1.5. Вычислить интеграл: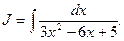

Решение. Данный интеграл имеет вид: 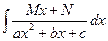, где 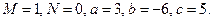Выделим в знаменателе дроби полный квадрат:

.

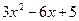
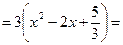
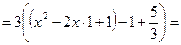
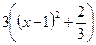Подставим подученную функцию вместо знаменателя дроби и проведем преобразования:

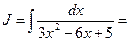
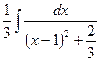
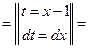
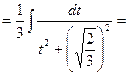
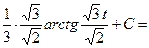
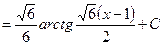(см. формулу 11).

Дата добавления: 2014-01-04