
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Диссипация на фронте ударной волны
|
|
|
|
а) Удельная величина диссипации энергии
На фронте ударной волны наблюдается скачок энтропии (рис.4.12),
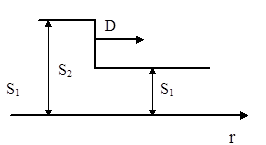 Рис. 4.12 Рис. 4.12
| то есть энергия направленного движения частиц частично переходит в энергию беспорядочного теплового движения, в результате чего кинетическая энергия соответствующего элемента среды уменьшается, а внутренняя энергия его возрастает. |
Увеличение энтропии на фронте ударной волны говорит о том, что имеют место необратимые диссипативные процессы, связанные с проявлением свойств вязкости и теплопроводности вещества в узкой зоне фронта ударной волны (см. п. 4.6 и 4.8).
Скачок энтропии характеризует степень необратимости потерь энергии (диссипации энергии). Если провести аналогию с механическими системами, то необратимые потери энергии при ударном сжатии подобны потерям энергии на трение при механическом движении.
Скачок энтропии при слабом ударном сжатии пропорционален третьей степени скачка давления на фронте ударной волны, то есть (см. (4.39))
S2 - S1 ~ (DP)3 = (P2 - P1)3.
По мере удаления фронта ударной волны от места ее возникновения все большая часть начальной энергии превращается в необратимые потери энергии.
Определим удельные потери энергии на фронте ударной волны, если заданы параметры этой волны.
Пусть DEп есть удельные необратимые потери энергии из расчета на
единицу массы данной среды для заданной ударной волны. Единица массы среды до ударного сжатия занимает объем 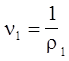 , в результате ударного сжатия объем единицы массы среды становится равным
, в результате ударного сжатия объем единицы массы среды становится равным  . После ударного сжатия эта элементарная масса среды совершает работу при изоэнтропическом расширении до объема
. После ударного сжатия эта элементарная масса среды совершает работу при изоэнтропическом расширении до объема 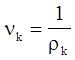 (рис.4.13).
(рис.4.13).
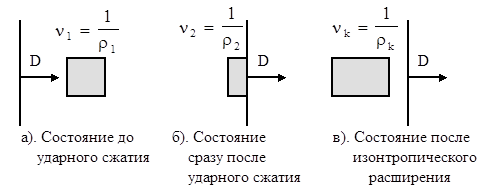
Рис. 4.13
Процесс ударного сжатия и последующего изоэнтропического расширения единицы массы среды можно представить графически (рис. 4.14). Состояние вещества до ударного сжатия (P1, n1) соответствует точ-
| ке 1, после ударного сжатия параметры данной частицы вещества скачком переходят в точку 2, лежащую на ударной адиабате 1 - 2 вещества, затем эта частица изоэнтропически расширяется вдоль изоэнтропы 2 - k (см. рис. 4.14). |  Рис. 4.14 Рис. 4.14
|
При ударном сжатии изменение внутренней энергии единицы массы равно (4.5)
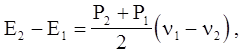 (4.48)
(4.48)
что соответствует на рис. 4.14 площади трапеции 1234.
После ударного сжатия частица среды совершает работу при изоэнтропическом расширении, при этом состояние частицы перемещается вдоль изоэнтропы от точки 2 до точки k. Для определения этой работы воспользуемся первым началом термодинамики
TdS = dE + Pdn
Так как расширение изоэнтропическое (S = const), то левая часть этого соотношения будет равна нулю (dS = 0), следовательно:
dE = - Pdn (4.49)
Проинтегрировав это выражение вдоль изоэнтропы, получим
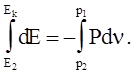 (4.50)
(4.50)
Очевидно, что в левой части интеграл равен разности энергий единицы массы в точках k и 2, то есть
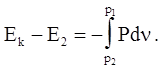 (4.51)
(4.51)
Запишем полученное выражение в виде
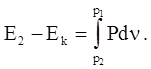 (4.52)
(4.52)
Совершенно очевидно, что необратимые потери энергии на фронте ударной волны будут равны разности работ при ударном сжатии и изоэнтропическом расширении, то есть разности соответственно левых и правых частей уравнений (4.48) и (4.52):
 (4.53)
(4.53)
Эта энергия расходуется на нагревание единицы массы при начальном давлении P1 от температуры T1 (точка 1 на рис. 4.14).Из соотношения (4.53) можно найти температуру среды после прохождения ударной волны. Например, для совершенного газа, поскольку
 (4.54)
(4.54)
интеграл
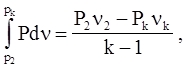 (4.55)
(4.55)
а при Pk = P1 (при этом nk > n1) получим
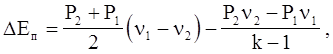 (4.56)
(4.56)
где nk может быть определено из соотношения
 (4.57)
(4.57)
С помощью соотношения (4.56) можно определить температуру среды после прохождения ударной волны. Для этого находим удельные необратимые потери энергии с помощью формулы
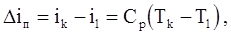 (4.58)
(4.58)
где Ср - удельная теплоемкость при постоянном давлении;
ik и i1 - теплосодержания, соответствующие состояниям среды в точках k и 1 (рис. 4.14).
Поскольку i = E + Pn, то Diп и DEп связаны между собой соотношением
 (4.59)
(4.59)
Учитывая формулы (4.56), (4.58) и (4.59), получим
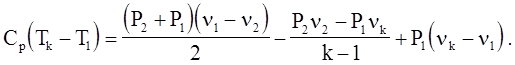
Отсюда можно определить температуру совершенного газа Тk после ударного сжатия и последующей изоэнтропической разгрузки до первоначального давления P1. Если же известна температура среды Tk, то с помощью формул (4.58) и (4.59) определяется удельная необратимая потеря энергии

б) Полная величина диссипации энергии
| Рассмотрим определение полной величины необратимых потерь энергии на примере сферической ударной волны. Полная величина необратимых потерь энергии есть функция радиуса фронта ударной волны R (рис. 4.15). Тогда элементарные энергетические потери при |  Рис. 4.15
Рис. 4.15
|
прохождении ударной волны через элементарный шаровой слой будут равны
 (4.60)
(4.60)
где Dm - масса данного элементарного слоя,
r 1 - плотность среды до ударного сжатия,
 - энергетические потери в данном элементарном шаровом слое.
- энергетические потери в данном элементарном шаровом слое.
Проинтегрировав это выражение по радиусу, получим полную величину необратимых потерь энергии для сферической ударной волны
 (4.61)
(4.61)
где r0 - начальный радиус ударной волны.
Для того чтобы определить полную величину энергетических потерь с помощью уравнения (4.61), нужно знать:
1) ударную адиабату данной среды (ударную адиабату Гюгонио)
P2 = P2(n2); (4.62)
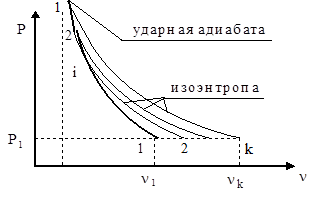 Рис. 4.16
Рис. 4.16
| 2) изоэнтропы разгрузки для данной среды, проходящие через разные точки ударной адиабаты (рис. 4.16) P = P(n); (4.63) 3) зависимость давления на фронте ударной волны от радиуса P2 = P2(r). (4.64) |
в) Приближенный расчет необратимых потерь энергии
Поскольку вычисление полной энергии диссипации Еп по формуле (4.61) представляет значительные трудности, рассмотрим приближенный способ вычисления величины Еп. . В этом случае выражение (4.61) заменяется приближенной формулой
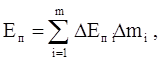 (4.65)
(4.65)
где DЕп i - удельные необратимые потери энергии в шаровом слое среды;
Dmi - масса i-го слоя среды.
Расчет проводится в следующем порядке. Сначала на миллиметровке вычерчивается ударная адиабата данной среды. На этой ударной адиабате выбирается достаточное количество точек и для каждой из этих точек строятся изоэнтропы разгрузки (см. рис. 4.16). Затем по этому графику для каждого значения давления на фронте ударной волны P2 i подсчитывают DЕп i, где i = 1, 2,... m.
 Рис. 4.17
Рис. 4.17
| 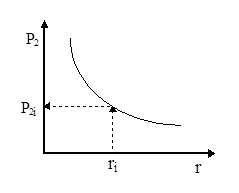 Рис. 4.18
Рис. 4.18
|
После этого строят график зависимости удельной диссипации энергии в ударной волне DЕп от давления на фронте ударной волны P2 (рис. 4.17). Далее для каждого i-го слоя подсчитывают его массу Dmi, которая зависит от радиуса ri (см. рис. 4.15). Каждому радиусу ri соответствует свое давление на фронте ударной волны P2i (рис. 4.18) и, следовательно, величина удельной энергии диссипации DЕп i (см. рис. 4.17).
Затем по формуле
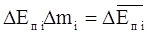 (4.66)
(4.66)
вычисляют необратимые потери энергии для каждого i-го шарового слоя и, наконец, просуммировав энергетические потери в разных слоях по формуле (4.65)
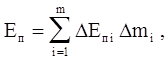
получают приближенное значение необратимых потерь энергии во всем объеме среды, имеющем радиус R (см. рис. 4.15).
Лекция №14.
План лекции
1. Ударные адиабаты
2. Уравнение состояния жидких и твердых сред
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 780; Нарушение авторских прав?; Мы поможем в написании вашей работы!