Твердых и жидких сред

Ударные адиабаты и уравнения состояния

а) Ударные адиабаты

Определение ударной адиабаты для совершенного газа было рассмотрено в п. 4.3. В этом случае ударная адиабата Гюгонио легко получается с помощью уравнения энергии на фронте ударной волны

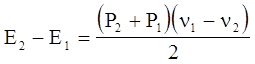(4.67)

и уравнения состояния совершенного газа

(4.68)

Для жидких и твердых тел, как правило, уравнения состояния P = P(r, E) неизвестны, поэтому получить ударную адиабату в этом случае невозможно с помощью уравнения (4.67).

В послевоенные годы были разработаны различные методы экспериментального определения параметров ударных волн с применением осциллографической, оптической или рентгеновской аппаратуры. Эти методы позволяют экспериментально получать ударные адиабаты различных твердых и жидких сред. На фронте ударной волны в идеальной среде законы сохранения импульса и массы (см. п. 4.2) выражаются уравнениями:

(4.69)

Эти уравнения, строго говоря, справедливы для жидкой среды. Для твердых же тел необходимо использовать два первых уравнения (4.7). В системе двух уравнений (4.69) четыре неизвестных D, u₂, P₂, r _4. Если из этих четырех неизвестных любые два, например D, u₂; P₂, u₂ или D, r ₂, определить экспериментально, то два других параметра определяются из уравнений (4.69).

Если измерять в данном веществе параметры ударных волн различной интенсивности, например D_i, u_{2 i},

где i = 1, 2,... n,

n - число опытов,

то зависимость D = D(u₂) представляет собой экспериментальную ударную адиабату в координатах D, u_4. В этом случае на основе уравнения D = D(u₂) с помощью (4.69) определяется ударная адиабата в виде P₂ = P₂(r ₂).

Для решения некоторых задач экспериментальную кривую ударной сжимаемости вещества удобно представить в виде

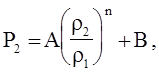(4.70)

где A, B и n - постоянные, которые для ряда веществ приведены в табл. 4.4.

Более точное уравнение для аппроксимации экспериментальных ударных адиабат может быть представлено в виде:

(4.71)

где a_k - постоянные коэффициенты, приведенные в табл. 4.3 для ряда металлов.

Таблица 4.2

Значения постоянных коэффициентов A, B и n для некоторых

твердых и жидких тел

Материал	A × 10^-3 кгс/см^2	B × 10^-3 кгс/см^2	n	Давление P2 × 10^-3 кгс/см
Сталь	553	-543	3	70-130
Сталь	142,5	-67,1	6	165-500
Сталь	231	-310	5,6	500-5000
Алюминий, дюралюминий	235	-240	3,8	40-700
Алюминий, дюралюминий	224	-298	4,1	700-2000
Медь	315	-315	4,65	190-1000
Медь	368	-580	4,75	1000-4300
Свинец	103	-103	4,8	200-500
Свинец	284	-515	3,5	1000-4250
Баллистический порох	5,42	-5,42	7,7	36-130
Вода	4,3	-4,3	6,4	30-115
Вода	140	-284	2	115-450

Таблица 4.3 Значение коэффициента a_k × 10 ^-10 дин/см²

k	Al	Cu	Pb	Fe
	73,1		41,1	30,3
	152,7	271,7	101,7	724,5
	143,5			-271,2
	-887		-43	-14
		-2967
	-3192		-801	—
		-1346		—

Между скоростью частиц за фронтом ударной волны u₂ и скоростью фронта D в различных веществах существует зависимость, близкая к линейной: D = c₀ + lu. (4.72)

Численные значения c₀ и l для некоторых веществ представлены в табл. 4.4 для ряда металлов.

Таблица 4.4

Значения коэффициентов c₀ и l

Материал	r 0, г/см^3	c0, м/сек	l	P2 × 10^-3, кгс/см^2
Сталь	7,85		1,58	400-5000
Сталь	7,85		1,58	1000-4100
Дюралюминий, алюминий	2,71-2,785		1,39	40-2000
Медь	8,90		1,497	220-1470
Медь	8,93		1,48	1000-4300
Свинец	11,34		1,517	200-1410
Свинец	11,34		1,26	1000-4250
Магний	1,72		1,16	60-400
Цинк	7,14		1,45	350-3300
Серебро	10,49		1,54	460-4100
Кадмий	8,64		1,48	360-3500
Золото	19,3		1,47	590-5200
Бериллий	1,845		1,091	144-290
Кобальт	8,82		1,33	246-1640
Хром	7,1		1,465	238-1400
Молибден	10,2		1,238	260-1670
Никель	8,86		1,445	240-1520
Титан	4,51		1,088	172-1080
Продолжение таблицы 4.4
Материал	r 0, г/см^3	c0, м/сек	l	P2 × 10^-3, кгс/см^2
Латунь	8,41		1,423	170-1800
Баллистический порох	1,58		1,86	36-130
Кристаллический гексоген	1,8		1,61	68-158
Литой тротил	1,62		1,41	61-142
Нитрометан	1,14		1,38	20-88
Сплав Вуда	9,7		1,03	150-400
Люцит	1,18		1,51	3-76
Песок	1,66		2,41	1-50
Песок	1,65		1,42	45-470
Песчаник сухой	—		1,4	—
мокрый	—		1,42	—

б) Уравнение состояния жидких и твердых сред

Современные теоретические методы физики высоких давлений и температур позволяют установить функциональные связи, например, между давлением, температурой и плотностью или между давлением, плотностью и внутренней энергией. Для получения же конкретных уравнений состояния определенных веществ необходимы некоторые экспериментальные данные. В настоящее время широкое распространение получили методы определения уравнений состояния вида P = P(r, T) или P = P(r, E) на основе экспериментальных данных по ударному сжатию вещества.

Рассмотрим один из распространенных методов определения уравнения состояния на основе известной опытной ударной адиабаты этого вещества. При этом не делают различия между твердым телом и жидкостью, а давление P в твердом теле в этом случае представляют как давление в условиях всестороннего сжатия.

Полные энергии E и давления P вещества могут быть представлены в виде суммы упругих (“холодных”) и тепловых составляющих:

(4.73)

где P_х, E_х - упругие части давления и энергии, определяемые воздействием частиц при Т = 0^°К;

P_т, E_т - тепловые составляющие давления и энергии, определяемые тепловым движением частиц (атомов, молекул);

P_е, Е_е - электронные составляющие давления и энергии, отвечающие тепловому возбуждению электронов, они имеют существенное значение при температуре свыше 10^4°К. Такая температура возникает при ударном сжатии металлов при давлении свыше 1 млн. атм. Для более низких температур и давлений уравнения (4.73) могут быть представлены в виде

(4.74)

Упругие составляющие давления P_х и энергии E_х cвязаны только с силами взаимодействия между частицами и не зависят от температуры, то есть P_х = P_х(n), E_х = E_х(n). Эти зависимости представляют собой изотермы при Т = 0^°К. Между P_х и E_х существует связь, вытекающая из первого начала термодинамики при Т = 0^°К, dE_х + P_хdn = 0:

(4.75)

(4.76)

где n_0K - удельный объем вещества при Т = 0^°К.

Тепловые составляющие давления P_т и энергии E_т Согласно теории твердого тела могут быть связаны следующей зависимостью

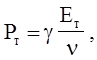(4.77)

где g = g(n) - коэффициент Грюнайзена, равный отношению теплового давления P_т к плотности тепловой энергии E_т / n. Формула (4.77) аналогична соответствующей формуле для совершенного газа , для которого все давление P теплового происхождения и g = k - 1.

Для твердых тел до P > 0,5 млн. атм. можно считать коэффициент Грюнайзена g равным его начальному значению g₀.

При давлениях ударного сжатия P ® ¥ атомы вещества полностью ионизируются, тепловое давление становится основным и вещество превращается в газ с показателем k = 5 / 3, при этом предельное значение коэффициента g_пр = k - 1 = 2 / 3.

Величина P_т согласно (4.74) равна

(4.78)

Дифференцируя это соотношение, найдем

(4.79)

Согласно термодинамическому равенству

коэффициент g для начальных условий можно записать в виде

(4.80)

где 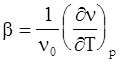- объемный коэффициент теплового расширения,

- модуль объемного сжатия.

Для нормальных условий g(n₀) для металлов колеблется от 1 до 3. При увеличении давления P ® ¥ g ® 2/3. Коэффициент Грюнайзена g связан с давлением упругого сжатия P_х и удельным объемом n с помощью следующей формулы:

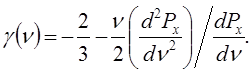(4.81)

Связь электронных членов P_е и Е_е при температуре не выше нескольких десятков тысяч градусов, имеет вид:

(4.82)

где b₀ - коэффициент электронной теплоемкости при нормальном объеме, он берется на основании измерения теплоемкости при очень низких температурах.

Рис. 4.19

Рассмотрим графическую интерпретацию уравнений (4.74) на рис. 4.19. Кривая ed представляет собой нулевую изотерму Px = Px(n), ас - ударную адиабату. Разница между кривыми ас и ed численно равна тепловой составляющей давления Pт. Площадь под кривой Px = Px(n) соответствует величине упругой энергии

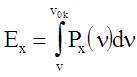. Площадь асed, заштрихованная на рис. 4.19, представляет собой приращение тепловой энергии Е_т - Е₀. Действительно, согласно (4.74) Е = Е_х + Е_т , на фронте ударной волны 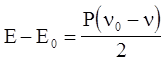(при P₀» 0) и, следовательно,

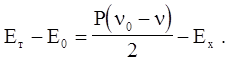(4.83)

Величина соответствует площади треугольника abc (см. рис. 4.19), а разница ^{— Ex} представляет собой заштрихованную площадь асed, равную приращению тепловой энергии Е_т - Е₀.

Определим связь между тепловой частью энергии Е_т и температурой Т. Теплоемкость . В определенном диапазоне температур Т - Т₀ можно приближенно считать, что C_v = const, в этом случае

(4.84)

где 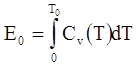- тепловая энергия при комнатной температуре. Уравнения (4.73) с учетом (4.76), (4.77), (4.82), (4.84) могут быть записаны в виде:

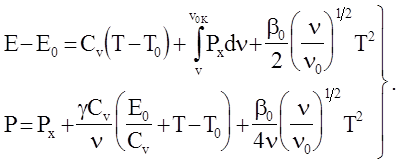(4.85)

Левая часть первого уравнения (см. уравнение (4.67)).

Если к двум уравнениям (4.85) прибавить (4.81), то получим систему из трех уравнений с тремя неизвестными P_x, g, T при условии, что известна зависимость P = P(n), представляющая собой экспериментальную ударную адиабату. Для каждой пары численных данных P_i, n_i из уравнений (4.81), (4.85) можно получить численные значения P_{x i} , g_i , T_i с помощью решения этих уравнений на ЭВМ. Повторяя такой расчет n раз, получим уравнение состояния вещества в табличной форме P_i , n_i , T_i (где i = 1, 2,... n). В таблице (4.5) даны эти расчетные данные для некоторых металлов.

Таблица 4.5. Расчетные данные для Al, Cu, Pb.

Металл	r / r 0	P×10^-3 кгс/см^2	Px × 10^-3 кгс/см^2	T°C	g
	1,1	91,8	79,6		1,81
Al	1,35	48,2			1,31
	1,8				1,3
	1,1				1,85
Cu	1,2				1,88
	1,7				1,54
	1,2				—
Pb	1,4				—
	2,2				—

Полученные таким образом зависимости P_x = P_x(r) и g = g(r) могут быть с любой точностью аппроксимированы уравнениями:

(4.86)

На основании этих функций можно уравнения состояния жидких и твердых тел записать в следующей форме:

(4.87)

где 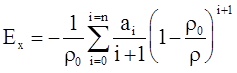(см. уравнение (4.76)).

Уравнение (4.87) можно получить и иначе, если известна ударная адиабата P = P(n), E = E(n) и g = g(n) (или g = g₀ = const). Так как , то определяя Е_х из (4.87), получим

(4.88)

Интегрируя это уравнение, получим P_x = P_x(n), а затем и E_х = E_х(n) по формуле (4.76).

Дата добавления: 2014-01-04