Квадратичные формы

Линейная модель обмена

Лекция 9

Оценка эффективности защиты информации в сетях и системах ПД.

В период эксплуатации периодически должны проводиться специ­альные обследования и проверки выделенных помещений и объектов ТСТ1И.

Спецобследование здания должно проводиться во всех служебных помещениях учреждения (не только выделенных) сотрудниками органа по защите информации. Спецобследование должно проводиться под легендой для сотрудников учреждения или в их отсутствие (допускается присутствие ограниченного круга лиц из числа руководителей учрежде­ния и сотрудников службы безопасности).

Спецобследование должно проводиться с использованием оборудования, прошедшего сертификацию в установленном порядке.

3. Тенденции и перспективы совершенствования теории и техники средств, используемых для обеспечения информационной безопасности в различных системах связи и телекоммуникации.

Основная тенденция – применение современных, сертифицированных средств защиты информации отечественного производства, автоматизация процесса контроля эффективности мер защиты информации.

Перспектива – комплексный подход к защите информации (применение комплекса органиизационных и технических мероприятий), использование многофункциональных технических средств, комплексирование и автоматизация процессов контроля эффективности мер защиты и непосредственно защиты информации.

Вопросы для повторения:

1. Этапы организации работ по защите информации от утечки по техническим каналам на объектах ТСПИ и их содержание.

2. Мероприятия первого этапа работ по защите информации.

3. Мероприятия второго этапа работ по защите информации.

4. Мероприятия третьего этапа работ по защите информации.

5. Организация контроля в ходе реконструкции объекта.

Тема: “Квадратичные формы.

(модель международной торговли)”

Пусть вектор , где 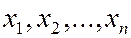- координаты этого вектора в некотором базисе .

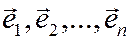Определение 1. Квадратичной формой называется линейная функция переменных, которая определяется как сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:

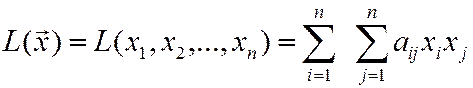. (1)

Коэффициенты квадратичной формы 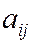- действительные числа, причем . Матрица , составленная из этих коэффициентов, называется матрицей квадратичной формы.

В матричной записи квадратичная форма имеет вид:

, (2)

где 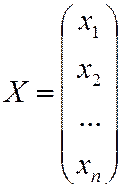- столбец переменных.

Определение 2. Квадратичная форма называется невырожденной, ес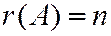ли или 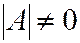. Рангом квадратичной формы называется ранг матрицы .

Чтобы составить матрицу квадратичной формы, следует на ее диагонали поместить коэффициенты при квадратах переменных, а коэффициенты при произведениях различных переменных разделить пополам и эти «половинки» разместить симметрично главной диагонали.

Пример 1. Дана квадратичная форма

.

Записать ее в матричном виде.

Решение: Найдем матрицу квадратичной формы.

.

Поэтому

.

Вид матрицы квадратичной формы определяется базисом 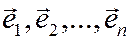, в котором задан вектор 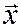и меняется при переходе к другому базису по формуле:

, (3)

где 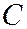- матрица перехода от старого базиса к новому.

Определение 3. Квадратичная форма

называется канонической (или имеет канонический вид), если все ее коэффициенты 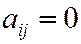при :

,

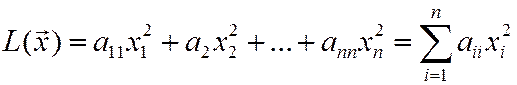а ее матрица является диагональной.

Теорема 1. Любая квадратичная форма может быть приведена к каноническому виду.

Пример 2. Привести к каноническому виду квадратичную форму

.

Решение: Выделим полный квадрат при переменной , затем при :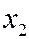

.

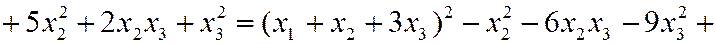
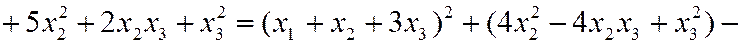
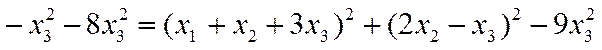Переход к новым переменным:

, , .

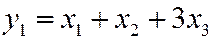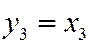приводит данную квадратичную форму к каноническому виду

.

Замечание: Канонический вид квадратичной формы не является однозначно определенным, так как одна и та же квадратичная форма может быть приведена к каноническому виду разными способами.

Свойства квадратичной формы:

1) Теорема (закон инерции квадратичных форм). Число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы, приведенной к каноническому виду, не зависит от способа приведения формы к этому виду.

2) Ранг матрицы квадратичной формы равен числу отличных от нуля коэффициентов канонической формы и не меняется при любых преобразованиях.

Определение. Квадратичная форма называется положительно (отрицательно) определенной, если при всех значениях переменных, из которых хотя бы одно отлично от нуля,

().

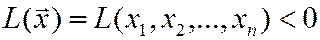Теорема. Для того чтобы квадратичная форма была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения 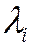матрицы были положительны (отрицательны).

Для установления знакоопределенности квадратичной формы применяют критерий Сильвестра.

Теорема (критерий Сильвестра). Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительны, т.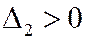е. , ,…, , где

.

Следует отметить, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, начиная со знака «минус» для минора первого порядка.

Пример. Доказать, что квадратичная форма является положительно определенной.

Решение.Первый способ. Матрица квадратичной формы имеет вид 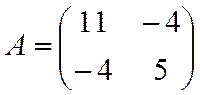. Для матрицы характеристическое уравнение

или .

Найдем 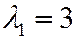, 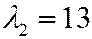. Так как корни характеристического уравнения матрицы положительны, то квадратичная форма - положительно определенная.

Второй способ. Так как главные миноры матрицы положительны:

, ,

то, по критерию Сильвестра, данная квадратичная форма положительно определенная.

Дата добавления: 2014-01-04