Линейная модель обмена

Пусть имеется стран 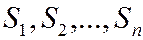, национальный доход каждой из которых равен соответственно . Обозначим коэффициентами 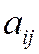долю национального дохода, которую страна 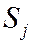тратит на покупку товаров у страны 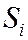. Будем считать, что весь национальный доход тратится на закупку товаров либо внутри страны, либо на импорт из других стран, т.е.

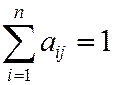(). (1)

Рассмотрим матрицу

,

которая назвается структурной матрицей торговли. В соответствии с (1) сумма элементов любого столбца матрицы равна 1.

Для любой страны 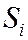(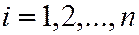) выручка от внутренней и внешней торговли составит:

.

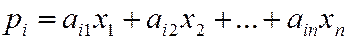Для сбалансированной торговли необходима бездефицитность торговли каждой страны 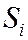, т.е. выручка от торговли каждой страны должна быть не меньше ее национального дохода:

().

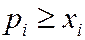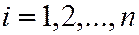Если считать, что (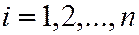), то получаем систему неравенств

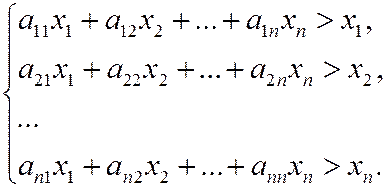(2)

Сложив все неравенства системы (2), получим после группировки

.

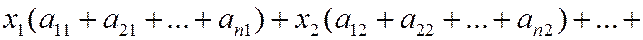
Учитывая (1), выражения в скобках равны единице, и получаем противоречивое неравенство

.

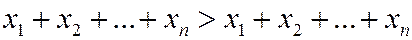Таким образом, неравенство (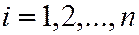) невозможно, и условие 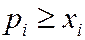принимает вид:

().

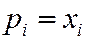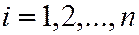С экономической точки зрения это понятно, так как все страны не могут одновременно получать прибыль.

Вводя вектор 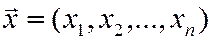национальных доходов стран, получим матричное уравнение

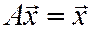(3)

Т.е. задача свелась к отысканию собственного вектора матрицы , отвечающего собственному значению .

Пример. Структурная матрица торговли трех стран имеет вид:

.

Найти соотношение национальных доходов стран для сбалансированной торговли.

Решение. Находим собственный вектор 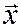, отвечающий собственному значению , решив систему

методом Гаусса. Найдем 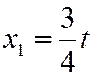, , , 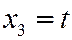т.е. .

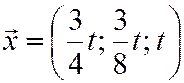Полученный результат означает, что сбалансированность торговли трех стран достигается при векторе национальных доходов 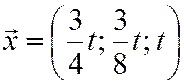, т.е. при соотношении национальных доходов стран или .

Дата добавления: 2014-01-04