Программная реализация RSA примерно в 100 раз медленнее программной реализации DES

Недостаток

Криптосистемы RSA реализуются как аппаратным, так и программным путем.

Теперь разработчикам криптоалгоритмов с открытым ключом на базе RSA приходится избегать применения чисел длиной менее 200 десятичных разрядов. Самые последние публикации предлагают применять для этого числа длиной не менее 250-300 десятичных разрядов.

В сделана попытка расчета оценок безопасных длин ключей асимметричных криптосистем на ближайшие 20 лет исходя из прогноза развития компьютеров и их вычислительной мощности, а также возможного совершенствования алгоритмов факторизации. Эти оценки даны для трех групп пользователей (индивидуальных пользователей, корпораций и государственных организаций), в соответствии с различием требований к их информационной безопасности. Конечно, данные оценки следует рассматривать как сугубо приблизительные, как возможную тенденцию изменений безопасных длин ключей асимметричных криптосистем со временем.

Таблица. Оценки длин ключей для асимметричных криптосистем, бит

Год	Отдельные пользователи	Корпорации	Государственные организации

Для аппаратной реализации операций шифрования и дешифрования RSA разработаны специальные процессоры. Эти процессоры, реализованные на сверхбольших интегральных схемах (СБИС), позволяют выполнять операции RSA, связанные с возведением больших чисел в колоссально большую степень по модулю N, за относительно короткое время.

И все же аппаратная реализация RSA примерно в 1000 раз медленнее аппаратной реализации симметричного криптоалгоритма DES.

Одна из самых быстрых аппаратных реализаций RSA с модулем N=512 бит на сверхбольшой интегральной схеме имеет быстродействие 64 Кбит/с. Лучшими из серийно выпускаемых СБИС являются процессоры фирмы CYLINK, выполняющие 1024-битовое шифрование RSA.

асимметричная криптосистема RSA имеет малое быстродействие по сравнению с симметричными криптосистемами.

С развитием технологии эти оценки могут несколько изменяться, но асимметричная криптосистема RSA никогда не достигнет быстродействия симметричных криптосистем.

Следует отметить, что малое быстродействие криптосистем RSA ограничивает область их применения, но не перечеркивает их ценность.

СХЕМА ШИФРОВАНИЯ ЭЛЬ ГАМАЛЯ

Схема Эль Гамаля (ElGamal), предложенная в 1985 г., может быть использована как для шифрования, так и для цифровых подписей.

Безопасность схемы Эль Гамаля обусловлена сложностью вычисления дискретных логарифмов в конечном поле.

Для генерации пары ключей (открытый ключ – секретный ключ), сначала выбирают некоторое большое простое число Р и большое целое число G, причем G<P.

Числа Р и G могут быть распространены среди группы пользователей.

Затем выбирают случайное целое число X, причем Х<Р.

Число X является секретным ключом и должно храниться в секрете.

Далее вычисляют

Y=G^x (mod P).

Число Y является открытым ключом.

Для того чтобы зашифровать сообщение PT, выбирают случайное целое число K, 1<K<Р-1, такое, что числа НОД (K,(Р-1))=1.

Затем вычисляют числа

а = G^K (mod Р),

b =Y^K × PT (mod P).

Пара чисел (a, b) является шифртекстом.

Заметим, что длина шифртекста вдвое больше длины исходного открытого текста PT.

Для того чтобы дешифровать шифртекст (а, b), вычисляют

PT = b/a^x (mod P). (*)

Поскольку

,

,

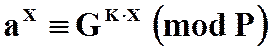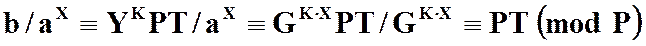то соотношение (*) справедливо.

Дата добавления: 2014-01-04