Лекция 15. Решение игр в смешанных стратегиях

15.1. Постановка задачи

При отсутствии седловой точки среди чистых стратегий приходится искать таковую среди смешанных. Применение минимаксных стратегий обеспечивает первому игроку выигрыш не меньше α, а второму – проигрыш не больше β. Поскольку α < β, для игрока 1 естественно желание увеличить выигрыш, а для игрока 2 – уменьшить проигрыш. Поиск такого решения приводит к использованию сложной стратегии, состоящей в случайном применении двух или более чистых стратегий с определенными частотами. Такая сложная стратегия в теории игр называется смешанной. Каждый из игроков применяет свои стратегии независимо от другого игрока.

Смешанной стратегией игрока А называется применение чистых стратегий A₁, A₂, …,A_m c вероятностями p₁, p₂, …,p_m.

Смешанную стратегию первого игрока обозначают как вектор:

P = (p₁, p₂,…,p_m), где p₁ + p₂ +…+ p_m = 1 и p₁, p₂, …,p_m ≥0

Смешанной стратегией игрока B называется применение чистых стратегий B₁, B₂, …,B_n c вероятностями q₁, q₂, …,q_n.

Смешанную стратегию первого игрока обозначают как вектор:

Q = (q₁, q₂,…,q_n), где q₁ + q₂ +…+ q_n = 1 и q₁, q₂, …,q_n ≥0

Если игрок 1 прибегает к своему выбору i с вероятностью p_i, а игрок 2 - к своему j -му выбору с вероятностью q_j, то, поскольку стратегии выбираются игроками независимо, вероятность выбора пары стратегий равна произведению x_i, y_j, и математическое ожидание выигрыша игрока 1 в смешанных стратегиях { P,Q } равно .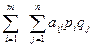

Игра имеет решение в смешанных стратегиях, если есть такие оптимальные стратегии x ^*, y ^* и число G такое, что при любых смешанных стратегиях x и y выполняется соотношение

G(x,y^*)≤G≤G(x^*,y)

Применение оптимальной смешанной стратегии обеспечивает игроку максимальный средний выигрыш (или минимальный средний проигрыш), равный цене игры V, независимо от того, какие действия предпринимает другой игрок, если только он не выходит за пределы своих активных стратегий. Теорема фон Неймана утверждает, что любая матричная игра с нулевой суммой всегда имеет седловую точку, т.е. существуют векторы P и Q такие, что

(V - цена игры).

Поиск цены игры и соответствующих вероятностей сводится к решению пары двойственных задач:

Минимизировать V при условиях

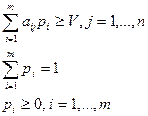
Максимизировать V при условиях

Если учесть, что при увеличении элементов матрицы A на любую константу С цена игры увеличится на С и это изменение не окажет влияния на искомые вероятности выборов, то всегда можно добиться положительности элементов матрицы и, следовательно, цены игры.

В предположении V > 0 можно провести замену переменных

Х_i = P_i / V, Y_j = Q _j / V

и поставленные задачи преобразовать к задачам с меньшим числом переменных:

Максимизировать при условиях

Минимизировать при условиях

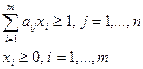
X – 1-й игрок, Y- 2-й игрок. Т.к игрок A старается увеличить свой выигрыш, т.е. цену игры v, то выражение 1/v будет стремиться к минимуму. Т.к игрок B старается уменьшить свой проигрыш, т.е. цену игры v, то выражение 1/v будет стремиться к максимуму

Пример 1. Для игры с матрицей

возникают задачи:

2-й игрок 1-й игрок

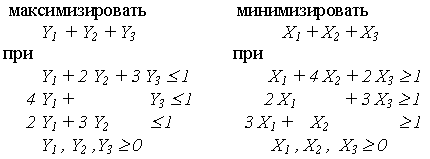
Решение этих задач симплексным методом дает оптимальные значения

X = { 11/37, 4/37, 5/37 }, Y = { 8/37, 7/37, 5/37 }

и экстремумы целевых функций, равные 20/37.

Отсюда

V = 37/20,
P = {11/20, 4/20, 5/20},
Q = {8/20, 7/20, 5/20},

Пример 2. Найти оптимальные стратегии и цену игры в игре 3×3 с платежной матрицей

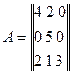
Сформулируем двойственные задачи линейного программирования

Максимизировать y1+y2+y3 при условиях 4y1+2y2 ≤1, 5y2 ≤1, 2y1+1y2+3y3≤1, yj≥0, j=1,2,3.

Минимизировать x1+x2+x3 при условиях 4x1 +2x3 ≥1, 2x1+5x2+1x3≥1, 3x3≥1, xi≥0, i=1,2,3.

Текст m.script

clc;

f=[1 1 1];

A=[4 2 0

0 5 0

2 1 3];

A=-A;

b=[1;1;1];

b=-b;

lb=[0 0 0];

X=linprog(f,A,b,[],[],lb,[]);

disp(X);

fopt=f*X;

v=1/fopt;

disp(v);

P=X/fopt;

disp(P);

Решение этих задач симплексным методом дает оптимальные значения

X = { 0.2903, 0.3871, 0.3226 }, V= 1.9355

Дадим объяснение полученному ответу. Выигрыш игрока А составит 60/31 ден.ед. Проигрыш игрока В составит 60/31 ден.ед. Игрок А: использует стратегию A₁ на 16.1290322580645 %; использует стратегию A₂ на 19.3548387096774 %; использует стратегию A₃ на 64.5161290322581 %.

Игрок B: использует стратегию B₁ на 29.0322580645161 %; использует стратегию B₂ на 38.7096774193548 %; использует стратегию B₃ на 32.258064516129 %.

Следует учесть, что мы здесь ограничиваемся рассмотрением игр, реализация которых может осуществляться любое число раз, не зависит от результата предыдущих действий и от длительности. Игры, где каждый последующий выбор зависит от результата предыдущих действий, относятся к т.н. многошаговым играм и не имеют столь простого решения [1].

Дата добавления: 2014-01-04