Основные понятия теории статистических решений

Теория статистических решений может быть истолкована как теория поиска оптимального недетерминированного поведения в условиях неопределенности. Согласно А. Вальду, поведение считается оптимальным, если оно минимизирует риск в последовательных экспериментах, т.е. математическое ожидание убытков статистического эксперимента. В такой постановке любая задача статистических решений может рассматриваться как игра двух лиц, в которой одним из игроков является "природа".

Иногда усредненные характеристики некоторого случайного процесса испытывают тенденцию к стабилизации и появляется возможность либо замены его детерминированным, либо использования каких-то методов исследования стационарных случайных процессов (методов теории массового обслуживания и др.).

Однако большинство процессов характеризуется "дурной неопределенностью", для которой невозможно найти законы распределения и другие вероятностные характеристики. В таких ситуациях приходится прибегнуть к экспертным оценкам.

Возникает и проблема выбора критерия оптимальности, поскольку решение, оптимальное для каких-то условий, бывает неприемлемым в других и приходится искать некоторый компромисс.

Пусть задан некоторый вектор S = (S₁,S₂,..,S_n), описывающий n состояний внешней среды, и вектор X=(X₁,X₂,..,X_m), описывающий m допустимых решений. Требуется найти вектор X^* =(0,0,..,0, X_i,0,..,0), который обеспечивает оптимум некоторой функции полезности W(X,S) по некоторому критерию K.

Информация oб указанной функции представляют матрицей размерности m x n c элементами W_ij=F(X_i,S_j), где F - решающее правило.

Рассмотрим следующую задачу [Шапкин]. Пусть, например, предприятие готовится к переходу на новые виды продукции (диверсификация производства), при этом возможны 4 решения P₁, P₂, P₃, P₄ , каждому из которых соответствует определенный вид выпускаемой продукции или их сочетание. Результаты принятия решений существенно зависят от неопределенных внешних условий (характеристик социально-экономической ситуации, например, макроэкономических факторов, структуры спроса на новую продукцию). Представим три типовых вариантов состояний внешней среды: П₁, П₂, П₃. Выигрыш, характеризующий относительную величину результата (доходы, прибыль и т.п.). соответствующих каждой паре сочетаний решений P и состояний внешней среды П, представлен в таблице 14.1.

Таблица 14.1.

Виды решений	Варианты внешней среды
П1	П2	П3
P1	0,25	0,35	0,20	0,25
P2	0,75	0,20	0,30	0,20
P3	0,35	0,80	0,10	0,10
P4	0,90	0,20	0,30	0,20

Нужно оптимальную стратегию P_i. Показатель эффективности

,

Для данной задачи E_V =max_i{0,25;0,20;0,10;0,20}=0,25,

Следовательно, предпочтение нужно отдать варианту P₁. При любом другом решении, в случае неблагоприятного состояния внешней среды, может быть получен выигрыш меньше 0,25. Критерий Вальда ориентирует ЛПР на слишком осторожную линию поведения, так как не учитывает, что, например, в случае принятия решений P₁ максимальный выигрыш не превышает 0,4. В то же время, при выборе решения P₄ при гарантированном выигрыше 0,2 можно в случае благоприятного состояния среды получить выигрыш, равный 0,9.

В ряде экономических задач в качестве критерия эффективности решений используется показатель минимума затрат. В таком случае критерий гарантированных затрат формулируется в виде

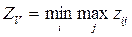
В качестве затрат могут выступать капитальные вложения, валовые издержки производства, приведенные годовые затраты, затраты на обеспечение качества продукции и другие показатели.

Рассчитаем выигрыши по критериям оптимизма, пессимизма, критерию минимального риска Сэвиджа, критерий обобщенного максимина (пессимизма-оптимизма) Гурвица.

Дата добавления: 2014-01-04