Системы координат на прямой, в плоскости и в пространстве

Элементы векторной алгебры

Простейшая задача аналитической геометрии

П 7.1 Ведение.

Аналитическая геометрия занимается исследованием геометрических форм с помощью алгебраического анализа.

В аналитической геометрии с помощью чисел характеризуется положение геометрических форм.

Определение:

Числа которые определяют положение геометрических форм называются координатами.

Определение:

Способ с помощью которого определяется положение геометрических форм называется методом координат.

Определение:

Начальная форма аналитической геометрии это точка и с помощью ее строят все остальные образы.

Определение:

Все линии и фигуры рассматриваются как геометрические места точек.

П 7.2 Системы координат на прямой

R1 – (множество чисел) обозначение числовой оси.

Система ординат на прямой задана если задана ось (горизонтальная прямая), начало и единица масштаба.

A(x) B(x) x

|AB|=|x₂-x₁|=|x₁-x₂|

Если направление отрезка с направлением оси то он положительный.

Определение:

Длина отрезка это всегда положительное число.

Определение:

Координатой точки А называется Х равное длине отрезка взятого со знаком плюс если направление совпадает с направление оси и наоборот со знаком минус если направление не совпадает с направлением оси.

На числовой оси установлено взаимнооднозначное соответствие множеством точек числовой оси и множеством действительных чисел.

П 7.3 Система координат на плоскости (R2)

Определение:

Система координат на плоскости считаем заданной, если заданы оси, начала координат и единица масштаба.

Определение:

Положительные точки на плоскости определяются двумя числами: абсциссой и ординатой.

Между точками (Х 0 У) и между парами действительных чисел установлено взаимнооднозначное соответствие.

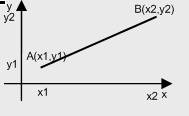
y

x

Определение:

Проекция отрезка на ось (0Х) называется число равное Х2-Х1

пр_хАВ=x2-x1=A1B1

Определение:

Проекция отрезка на ось (0У) называется число равное У2-У1.

Пр_y=y2-y1=A2B2

Проекции равны проекциям взятых со знаком + если направление отрезка совпадает с направление оси. И со знаком минус если противоположное.

П 7.4 Простейшие задачи аналитической геометрии

№1 расстояние между двумя точками на плоскости

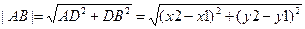(7.1)

Сумма квадратов разности соответствующих координат под корнем равна расстоянию между точками.

№2 деление отрезком в данном отношении

A(x1,y1)

B(x2,y2)

C(x,y)

Точка С делить отрезок АВ в отношении λ-лямбда.

Зная отношения в котором точка С делит АВ можно найти координату точки С

AA1||CC1||BB1 (АВ) (А1В1) делится на пропорциональные отрезки

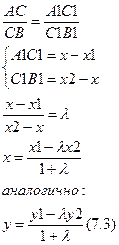
(7.3) справедливы при любом расположении точек АВС.

Дата добавления: 2014-01-04