
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод заміни змінної
|
|
|
|
Одним з основних методів обчислення інтегралів є метод заміни змінної. Заміна змінної в невизначеному інтегралі робиться за допомогою підстановок двох видів:
1) х= φ(t), де φ(t) – монотонна, неперервно диференційована функція нової змінної t. Формула заміни змінної в цьому випадку має вигляд
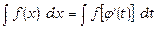 ;
;
2) u=ψ (x), де u – нова змінна. Формула заміни змінної при такій підстановці:
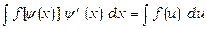 .
.
Ці формули показують, що при переході до нової змінної досить виконати заміну змінної у підінтегральному виразі.
Вдала заміна змінної дозволяє спростити початковий інтеграл, а у простіших випадках звести його до табличного.
Приклади 3. Знайти інтеграли
1) 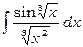
Зробимо підстановку 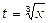 , тобто
, тобто 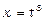 . Ця підстановка призведе до того, що під знаком синуса виявиться змінна інтегрування, а не корінь із неї. Знайдемо диференціал
. Ця підстановка призведе до того, що під знаком синуса виявиться змінна інтегрування, а не корінь із неї. Знайдемо диференціал 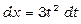 . Звідси одержуємо
. Звідси одержуємо
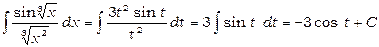 .
.
Відповідь повинна бути виражена через змінну х. Підставляючи в результат інтегрування 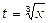 , одержимо
, одержимо
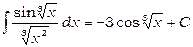 .
.
2) 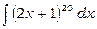 .
.
За допомогою заміни змінної можна відразу звести даний інтеграл до табличного. Покладемо 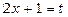 , тоді
, тоді 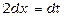 , тобто
, тобто 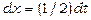 . Звідси одержуємо
. Звідси одержуємо
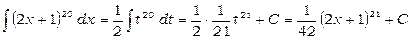 .
.
Взагалі, якщо інтеграл 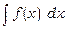 є табличним, то інтеграл
є табличним, то інтеграл 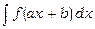 може бути легко знайдений за допомогою підстановки
може бути легко знайдений за допомогою підстановки 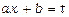 .
.
Наприклад, застосуємо цю підстановку до інтеграла 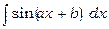 . Маємо
. Маємо 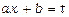 ,
, 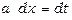 і
і 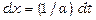 . Отже,
. Отже,
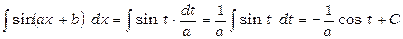 .
.
Повертаємося до минулої змінної, одержуємо
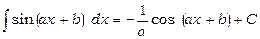 .
.
Аналогічно можна показати, що
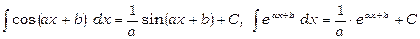 і т.п.
і т.п.
При знаходженні інтеграла 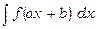 запису самої підстановки
запису самої підстановки 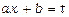 можна фактично й не робити. Тут досить взяти до уваги, що
можна фактично й не робити. Тут досить взяти до уваги, що 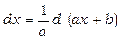 . Таким чином,
. Таким чином,
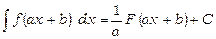 ,
,
де F – первісна для f.
3) 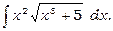
Покладемо 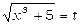 ; тоді
; тоді 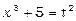 . Продиференціюємо обидві частини рівності:
. Продиференціюємо обидві частини рівності: 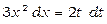 . Звідси
. Звідси 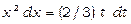 , отже,
, отже,
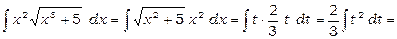

Даний інтеграл можна знайти й за допомогою підстановки 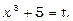 Ця підстановка відразу приводить інтеграл до табличного внаслідок того, що перший множник підінтегрального виразу
Ця підстановка відразу приводить інтеграл до табличного внаслідок того, що перший множник підінтегрального виразу 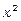 відрізняється від похідної підкореневого виразу
відрізняється від похідної підкореневого виразу 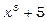 тільки постійним множником 1/3, тобто
тільки постійним множником 1/3, тобто 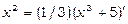 .
.
|
|
|
Взагалі, якщо підінтегральна функція є добутком двох множників, один з яких залежить від деякої функції ψ (х), а інший є похідною ψ (х) (з точністю до постійного множника), тоді доцільно зробити заміну змінної за формулою ψ (х) =t.
4) 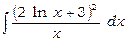 .
.
Перепишемо даний інтеграл у вигляді 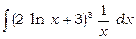 . Оскільки похідна виразу 2 1n x +3 дорівнює 2/ х, а другий множник 1/ х відрізняється від цієї похідної тільки постійним коефіцієнтом 2, тоді потрібно застосувати підстановку
. Оскільки похідна виразу 2 1n x +3 дорівнює 2/ х, а другий множник 1/ х відрізняється від цієї похідної тільки постійним коефіцієнтом 2, тоді потрібно застосувати підстановку 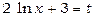 . Тоді
. Тоді 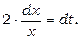
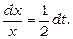 Отже,
Отже,
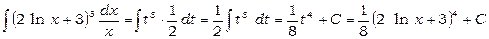 .
.
5) 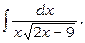
Зробимо підстановку 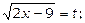 тоді
тоді 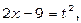
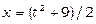 та
та 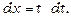 Отже,
Отже,
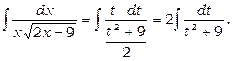
Застосувавши формулу 18, одержимо
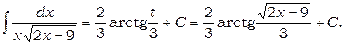
6) 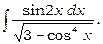
Зробимо підстановку 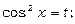 тоді
тоді 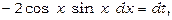 тобто
тобто 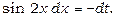 Знаходимо
Знаходимо
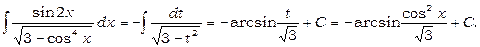
(ми використали формулу 20).
7) 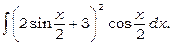
Застосуємо підстановку 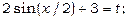 тоді
тоді 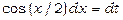 та
та
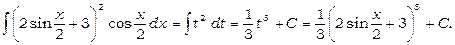
8) 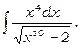
Застосуємо підстановку 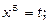 тоді
тоді 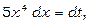
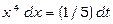 та
та
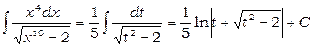
(див. формулу 21). Отже,
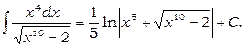
9) 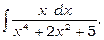
Перетворюючи знаменник дробу, одержимо 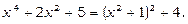 Зробимо підстановку
Зробимо підстановку  тоді
тоді 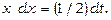 Звідси
Звідси
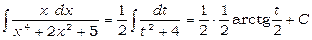
(див. формулу 18). Таким чином,
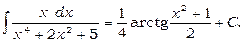
10) 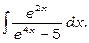
Покладемо 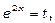 тоді
тоді 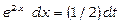 та
та
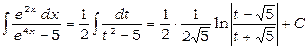
(ми застосували формулу 19). Отже,
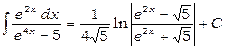 .
.
11) 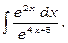
Зробивши таку ж підстановку, що й у попередньому прикладі, одержимо
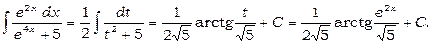
12) 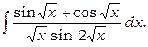
Покладемо 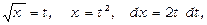 тоді одержимо
тоді одержимо
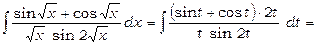
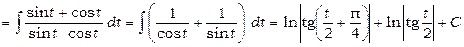
(див. формули 22 та 23). Повертаючись до минулої змінної, одержимо
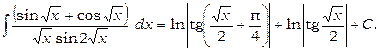
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 2117; Нарушение авторских прав?; Мы поможем в написании вашей работы!