
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Інтегрування тригонометричних функцій
|
|
|
|
1. Інтеграли виду 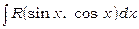 , де R – раціональна функція. Інтеграли зазначеного виду приводяться до інтегралів від раціональних функцій за допомогою так називаної універсальної тригонометричної підстановки
, де R – раціональна функція. Інтеграли зазначеного виду приводяться до інтегралів від раціональних функцій за допомогою так називаної універсальної тригонометричної підстановки  . У результаті цієї підстановки маємо:
. У результаті цієї підстановки маємо:

 .
.
Приклади 13. Знайти інтеграли
1) 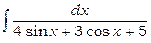 .
.
Підінтегральна функція раціонально залежить від 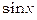 й
й 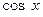 ; застосуємо підстановку
; застосуємо підстановку 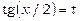 , тоді
, тоді 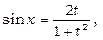

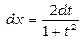 та
та
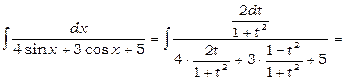
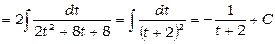 .
.
Повертаючись до минулої змінної, одержимо
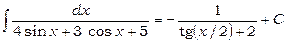 .
.
2) 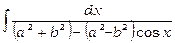 .
.
Покладемо 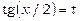 , тоді одержимо
, тоді одержимо
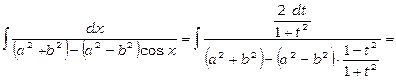
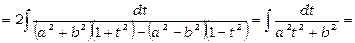
 .
.
Універсальна підстановка 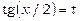 в багатьох випадках приводить до складних обчислень, тому що при її застосуванні
в багатьох випадках приводить до складних обчислень, тому що при її застосуванні 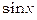 та
та 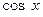 виражаються через t у вигляді раціональних дробів, що містять
виражаються через t у вигляді раціональних дробів, що містять  .
.
У деяких випадках знаходження інтегралів виду  може бути спрощено.
може бути спрощено.
1. Якщо  непарна функція відносно sin x, тобто якщо
непарна функція відносно sin x, тобто якщо 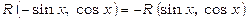 , то інтеграл раціоналізується підстановкою
, то інтеграл раціоналізується підстановкою  .
.
2. Якщо  непарна функція відносно cos x, тобто якщо
непарна функція відносно cos x, тобто якщо  , тоді інтеграл раціоналізується за допомогою підстановки
, тоді інтеграл раціоналізується за допомогою підстановки 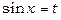 .
.
3. Якщо  парна функція відносно sin x й cos x, тобто якщо
парна функція відносно sin x й cos x, тобто якщо 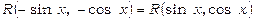 , тоді доцільно застосувати підстановку
, тоді доцільно застосувати підстановку  .
.
Приклади 14. Знайти інтеграли
1)  .
.
Оскільки підінтегральна функція непарна відносно синуса, тоді покладемо  . Звідси
. Звідси 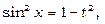
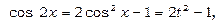
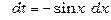 . Таким чином,
. Таким чином,
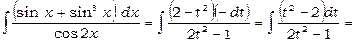
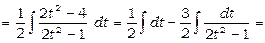
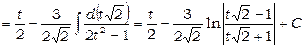 .
.
Отже,
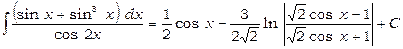 .
.
Відзначимо, що в розглянутому випадку інтеграл завжди може бути записаний у вигляді  .
.
2) 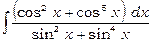 .
.
Тут підінтегральна функція є непарною відносно косинуса. Тому застосовуємо підстановку 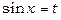 ; тоді
; тоді 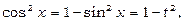
 . Отже,
. Отже,
 .
.
Оскільки  , то
, то
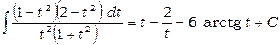 .
.
Остаточно одержуємо
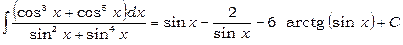 .
.
Відзначимо, що в розглянутому випадку інтеграл завжди може бути записаний у вигляді  .
.
3) 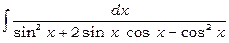 .
.
Підінтегральна функція парна відносно синуса та косинуса. Покладемо 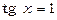 ; тоді
; тоді  ;
; 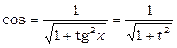 ;
;  . Звідси
. Звідси
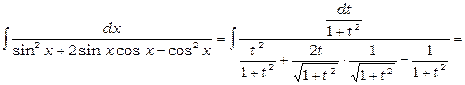
 .
.
Далі, маємо
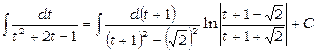 .
.
і, отже,
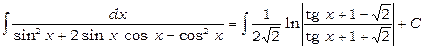 .
.
Відзначимо, що знаходження інтегралу можна спростити, якщо у вихідному інтегралі розділити чисельник і знаменник на  :
:
 .
.
2. Інтеграли виду 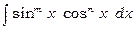 . Виділимо тут два випадки, що мають особливо важливе значення.
. Виділимо тут два випадки, що мають особливо важливе значення.
Випадок 1. Принаймні один з показників m або n – непарне додатне число.
Якщо n – непарне додатне число, то застосовується підстановка 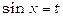 ; якщо ж m – непарне додатне число, - підстановка
; якщо ж m – непарне додатне число, - підстановка  .
.
Приклади 15. Знайти інтеграли
1)  .
.
Покладемо 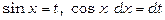 , тоді одержимо
, тоді одержимо
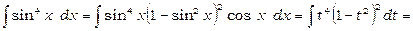
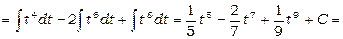
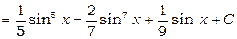 .
.
2) 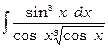 .
.
Маємо
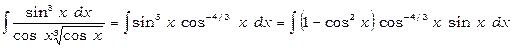 .
.
Якщо 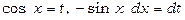 , тоді отримаємо
, тоді отримаємо
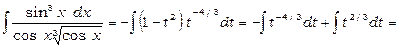
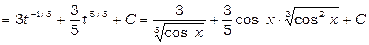 .
.
Випадок 2. Обидва показники ступеня m й n - парні додатні числа. Тут варто перетворити підінтегральну функцію за допомогою формул
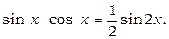 (1)
(1)
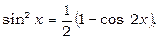 (2)
(2)
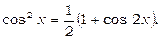 (3)
(3)
Приклади 16. Знайти інтеграли
1) 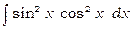 .
.
З формули (1) витікає, що
 .
.
Застосувавши формулу (2), одержуємо
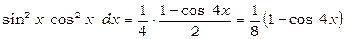 .
.
Отже,

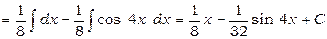 .
.
2) 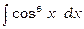 .
.
Використовуючи формулу (3), одержимо
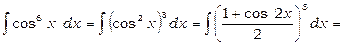
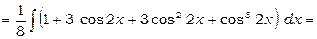
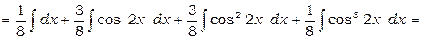
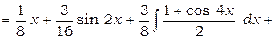
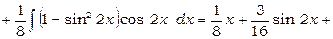
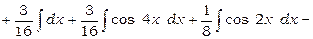
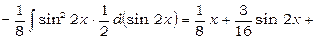
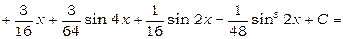
 .
.
3) 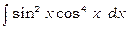 .
.
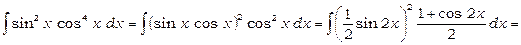
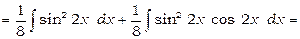
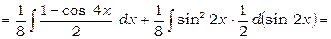
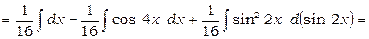
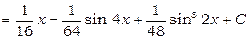 .
.
3. Інтеграли виду 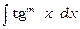 та
та  , де m – ціле додатне число. При знаходженні таких інтегралів застосовується формула
, де m – ціле додатне число. При знаходженні таких інтегралів застосовується формула  (або
(або  ), за допомогою якої послідовно знижується ступінь тангенса або котангенса.
), за допомогою якої послідовно знижується ступінь тангенса або котангенса.
Приклади 17. Знайти інтеграли
1)  .
.
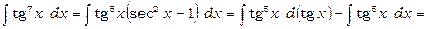
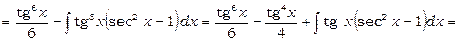
 .
.
2) 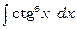 .
.
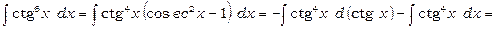
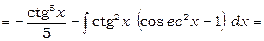
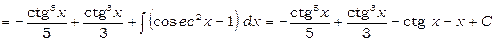 .
.
4. Інтеграли виду  й
й  , де п – парне додатне число. Такі інтеграли знаходяться аналогічно розглянутим у п. 3 за допомогою формули
, де п – парне додатне число. Такі інтеграли знаходяться аналогічно розглянутим у п. 3 за допомогою формули 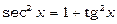 (або
(або 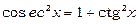 ).
).
Приклади 18. Знайти інтеграли
1)  .
.
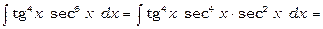
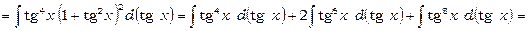
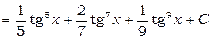 .
.
2)  .
.
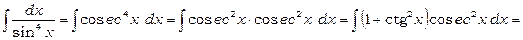
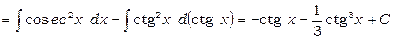 .
.
5. Інтеграли виду  й
й 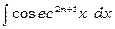 . Інтеграли від непарного додатного ступеня секанса або косеканса простіше всього знаходяться за рекурентними формулами:
. Інтеграли від непарного додатного ступеня секанса або косеканса простіше всього знаходяться за рекурентними формулами:
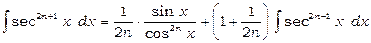 . (1)
. (1)
 . (2)
. (2)
Приклади 19. Знайти інтеграли
1) 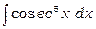 .
.
Застосовуючи рекурентну формулу (2) при  , тобто при
, тобто при 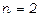 , одержимо
, одержимо
 ;
;
покладаючи 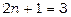 , тобто
, тобто 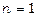 , за тією ж формулою маємо
, за тією ж формулою маємо
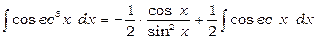 .
.
Оскільки  , тоді
, тоді
 ,
,
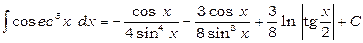 .
.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 11067; Нарушение авторских прав?; Мы поможем в написании вашей работы!