Спряжені простори. Приклади

ЛЕКЦІЯ 15

Підрахунок резервів зниження собівартості продукції

№	Назва резервів	Сума тис. грн
	Економія умовно-постійних витрат за умови збільшення обсягу випуску продукції	130,8
	Скорочення невиправданих перевитрат і непродуктивних витрат
	— матеріалів	95,3
	— заробітної плати	75,9
	— відрахувань на соціальні заходи	37,6
	— утримання й використання обладнання	14,5
	— цехових витрат	34,0
	— втрат від браку	34,0
	Усього	422,1

Вирішальною умовою використання виявлених резервів зниження собівартості продукції є підвищення продуктивності праці на основі досягнень науково-технічного прогресу. Запровадження нової техніки, комплексної механізації та автоматизації вироб­ничих процесів, удосконалення технології, запровадження прогресивних видів матеріалів, ліквідація втрат, удосконалення пла­нування, обліку й аналізу витрат забезпечуватимуть використан­ня наявних резервів і зниження собівартості продукції.

Для того щоб домогтися успіхів у майбутньому і не витрачати зайвого часу на виявлення резервів збільшення обсягу продукції і зниження собівартості за минулі періоди, необхідно систематично вести стратегічний оперативний, внутрігосподарський, порівняльний і функціонально-вартісний аналізи.

Тема: Спряжені простори та оператори. Їх властивості.

Приклади

Для лінійних функціоналів можна визначити операції додавання та множення їх на числа. Нехай ƒ₁ і ƒ₂ два лінійних функціонала в деякому лінійному просторі E.

Означення. Їх сумою ƒ₁+ƒ₂ називається лінійний функціонал

.

Означення. Добутком αƒ₁ лінійного функціонала ƒ₁ на число α називається функціонал

.

Рівності, що визначають ƒ₁+ƒ₂ і можна записати так:

, .

Зрозуміло, що сума ƒ₁+ƒ₂ і добуток αƒ₁ представляють собою лінійні функціонали. Крім того, якщо простір E метричний, то з неперервності функціоналів ƒ₁ і ƒ₂ слідує, що ƒ₁+ƒ₂ та αƒ₁ також неперервні на E.

Можна перевірити, що таким чином визначені операції додавання функціоналів та множення їх на число задовольняють всім аксіомам лінійного простору.

Означення. Сукупність всіх неперервних лінійних функціоналів, визначених на деякому лінійному метричному просторі E, утворює лінійний простір. Він називається простором, спряженим з E, та позначається E*.

Нехай початковий простір E нормований. Для неперервних лінійних функціоналів, заданих у нормованому просторі, ми ввели поняття норми, поклавши

Ця величина задовольняє всім аксіомам норми та умовам, які містяться в означенні нормованого простору. Дійсно,

1) , для будь-якого ненульового лінійного функціонала ƒ, ,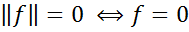

2) ,

Означення. Таким чином, простір E*, спряжений до нормованого простору, є нормованим простором. Якщо ми бажаємо підкреслити, що E* розглядається як нормований простір, замість E* іноді пишуть (E*, ).

Теорема. Спряжений простір (E*, ) є повним простором.

Дата добавления: 2014-01-04