Поняття системи лінійних рівнянь (СЛР) та її геометрична інтерпретація

ЛЕКЦІЯ 3: ЗАГАЛЬНА ТЕОРІЯ СИСТЕМ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ

Система m лінійних рівнянь з n невідомими записується у вигляді:

(2.1)

де 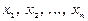– невідомі системи, – коефіцієнт при невідомій x_j в і -му рівнянні, b_і – вільний коефіцієнт в і -му рівнянні.

Матрицею СЛР (1) називається матриця коефіцієнтів при невідомих, тобто

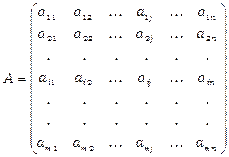
Вектором невідомих називається вектор , вектором вільних членів називається вектор .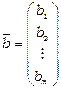

Розширеною матрицею СЛР (2.1) називається матриця

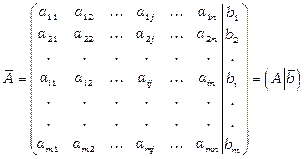
Очевидно, між системами лінійних рівнянь та їх розширеними матрицями існує взаємно однозначна відповідність (тобто по системі однозначно виписується розширена матриця, та по розширеній матриці однозначно виписується система).

За допомогою введених понять СЛР (2.1) можна подати у наступному матричному вигляді:

(2.2)

Тут ліва частина є матричним добутком матриці А розмірності 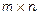та матриці-стовпчика 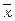розмірності 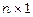, а рівність означає рівність двох матриць 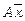та 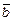розмірності .

Приклад 1. Записати у матричному вигляді СЛР:

Очевидно, матриця системи 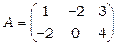, стовпчик вільних членів 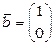, отже, система у матричному вигляді записується:

.

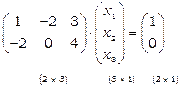Очевидно, виконуючи операцію множення матриць, отримаємо початкову СЛР.

Однорідною називається система лінійних рівнянь, що має нульовий стовпчик вільних членів, .

Неоднорідною називається система лінійних рівнянь, хоча б один елемент стовпчика вільних членів якої є ненульовим.

Розв’язком системи лінійних рівнянь, що містить n невідомих, називається впорядкований набір з n дійсних чисел – n -вимірний вектор , при підстановці яких в кожне рівняння системи замість відповідних змінних всі рівняння перетворюються на числові тотожності.

За множиною розв’язків системи поділяють на наступні види.

Система лінійних рівнянь називається сумісною, якщо має хоча б один розв’язок, та несумісною, якщо розв’язків не має.

Сумісна система лінійних рівнянь називається визначеною, якщо має єдиний розв’язок, та невизначеною, якщо розв’язків більше одного.

Проілюструємо введені поняття на системі з прикладу 1.

Очевидно, система є неоднорідною, сумісною (наприклад, легко перевірити, що вектор 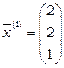є розв’язком системи) та невизначеною, оскільки можна перевірити, що вектор 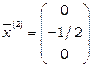також є її розв’язком.

Зауваження. Очевидно, однорідна СЛР завжди сумісна, оскільки нульовий вектор завжди є її розв’язком.

Дата добавления: 2014-01-04