Рівняння у повних диференціалах

Диференціальне рівняння вигляду

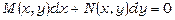, (13.19)

називається рівнянням у повних диференціалах, якщо 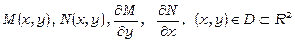- неперервні функції, причому

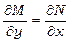. (13.20)

Назва рівняння пояснюється тим, що при виконанні умови (13.20) ліва частина рівняння (13.19) є повним диференціалом, тобто існує така диференційовна функція 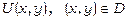, що має місце рівність

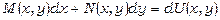, (13.21)

Доведемо, що (13.20) є необхідною і достатньою умовою (13.21). Дійсно, нехай виконується (13.21), тоді 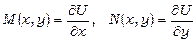, звідки 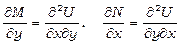. В силу неперервності частинних похідних маємо 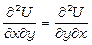, тому .

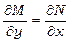Нехай виконується умова (13.20). Побудуємо деяку диференційовну функцію 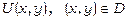таку, щоб мало місце (13.21) або .

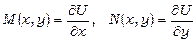Із першої рівності маємо:

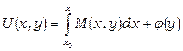, (13.22)

де 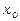- абсциса будь-якої точки з області існування розв’язку рівняння. При інтегруванні по 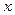змінна 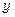вважається параметром, тому і довільна стала інтегрування має залежати від 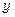. Підберемо функцію так, щоб виконувалось 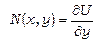. Для цього диференціюємо (13.22) по :

,

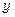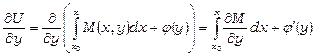тоді з врахуванням (20)

; ;

; .

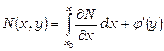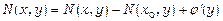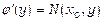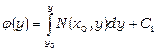Отже, шукана функція матиме вигляд

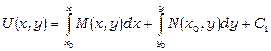, (13.23)

де 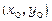- деяка точка з області існування розв’язку диференціального рівняння. Нагадаємо, що (23) – це функція, диференціал якої дорівнює лівій частині рівняння (19), тому загальний інтеграл цього рівняння має вигляд 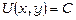або

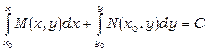. (13.24)

Зауважимо, що при практичному використанні формул (13.22), (13.23), (13.24) можна обчислювати невизначені інтеграли замість визначених.

Якщо умова (13.20) не виконується, то інколи вдається підібрати таку функцію 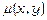, після множення на яку всіх частин рівняння (13.19) ліва частина цього рівняння стає повним диференціалом. Функція 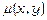називається інтегрувальним множником рівняння (13.19).

Помножимо (13.19) на :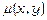

.

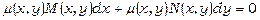Це рівняння буде рівнянням у повних диференціалах, якщо 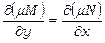, тобто

; ;

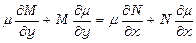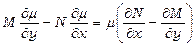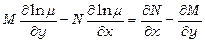. (13.25)

Рівняння (13.25) є диференціальним рівнянням у частинних похідних відносно невідомої функції 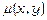. Доведено, що при певних умовах це рівняння має безліч розв’язків, тобто 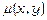існує, але у загальному випадку задача (13.25) складніша, ніж задача (13.19).

Розглянемо частинні випадки. Нехай 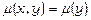, тоді 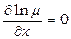, а співвідношення (13.25) набуде вигляду

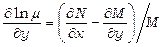. (13.26)

Якщо права частина рівності (13.26) не залежить від змінної 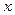, то

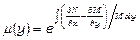. (13.27)

Аналогічно, якщо 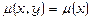, то інтегрувальний множник обчислюється за формулою:

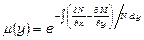. (13.28)

Приклад 12. Розв’язати диференціальне рівняння .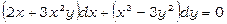

Дане рівняння є рівнянням у повних диференціалах, бо виконується умова (20), дійсно

.

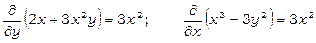Застосуємо формулу (22) для знаходження функції :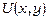

,

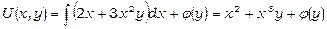звідки в силу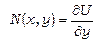

; ; .

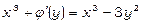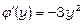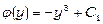Отже, 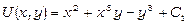, тому загальним інтегралом рівняння є

.

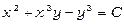Приклад 13. Розв’язати диференціальне рівняння .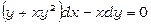

Для даного рівняння не виконується умова (13.20), бо

.

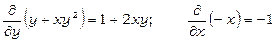Складемо вираз, що є лівою частиною співвідношення (13.26):

,

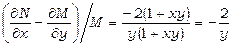звідки маємо ; .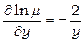

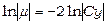Вибираємо 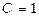і одержуємо шуканий інтегрувальний множник 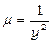. Помножимо початкове рівняння на : .

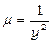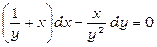Для цього рівняння умова повного диференціала (13.20) справджується, тому

;

; ; .

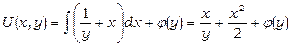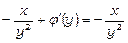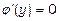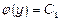Отже, загальний інтеграл рівняння .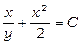

Приклад 14. Розв’язати диференціальне рівняння .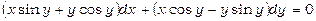

Для даного рівняння не виконується умова (13.20), бо

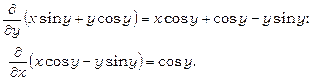
Шукаємо інтегрувальний множник рівняння, припускаючи що :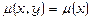

,

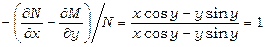звідки маємо ; ; 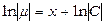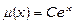. Вибираємо 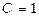та множимо початкове рівняння на :

.

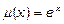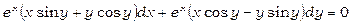Легко перевірити, що останнє рівняння є рівнянням в повних диференціалах, тому маємо

.

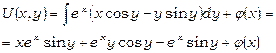Знайдемо похідну по 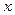від одержаної функції:

.

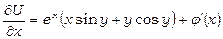Скориставшись рівністю 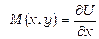, одержимо

,

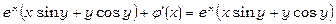звідки 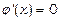, тобто 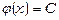. Остаточно маємо загальний інтеграл рівняння:

.

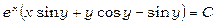Дата добавления: 2014-01-04