Потоки платежів. Фінансова рента

Контракти, угоди, комерційні та виробничо-господарські операції часто припускають не окремі разові платежі, а велику кількість розподілених у часі виплат та надходжень. Окремі елементи такого ряду, а інколи й сам ряд платежів у цілому, називається потоком платежів. Члени потоку платежів можуть бути як додатними (надходження), так і від’ємними (виплати) величинами. Потік платежів, всі члени якого додатні величини, а часові інтервали між двома послідовними платежами постійні, називають фінансовою рентою. Ренти діляться на річні та р -термінові, де р характеризує число виплат протягом року. Це дискретні ренти. У фінансово-економічній практиці зустрічаються і з послідовностями платежів, які відбуваються так часто, що практично їх можна розглядати як неперервні. Такі платежі описуються неперервними рентами.

Приклад 1. Нехай в конці кожного року протягом чотирьох років до банку вноситься по 1 млн. грош. од., відсотки нараховуються в кінці року, ставка - 5% річних. У цьому випадку перший внесок перетвориться до кінця терміну ренти на величину 10⁶´1,05³, оскільки відповідна сума була на рахунку протягом 3 років, другий внесок збільшиться до 10⁶´1,05², оскільки був на рахунку 2 роки. Останній внесок відсотків не приносить. Таким чином, в кінці терміну ренти внески з нарахованими на них відсотками являють собою ряд чисел: 10⁶´1,05³; 10⁶´1,05²; 10⁶´1,05; 10^6. Нарощена до кінця терміну ренти величина буде дорівнювати сумі членів цього ряду. Узагальнимо сказане, виведемо відповідну формулу для нарощеної суми річної ренти. Позначимо: S - нарощена сума ренти, R - розмір члена ренти,
i - ставка відсотка (десятковий дріб), n - термін ренти (число років). Члени ренти будуть приносити відсотки протягом n- 1, n- 2,..., 2, 1 і 0 років, а нарощена величина членів ренти складе

R (1+ i) ^{n -1}, R (1+ i) ^{n -2},..., R (1+ i), R.

Перепишемо цей ряд у зворотному порядку. Він представляє собою геометричну прогресію зі знаменником (1+ i) та першим членом R. Знайдемо суму членів прогресії. Отримаємо:

.

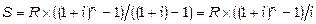Позначимо і будемо називати його коефіцієнтом нарощення ренти. Якщо ж відсотки нараховуються m разів на рік, то , де i - номінальна ставка відсотка.

Величина називається коефіцієнтом приведення ренти. Коефіцієнт приведення ренти при n ®¥ показує, у скільки разів сучасна величина ренти більше її члена:

.

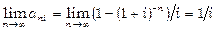Приклад 2. Під вічною рентою розуміють послідовність платежів, число членів якої не обмежено - вона виплачується протягом нескінченого числа років. Вічна рента не є чистою абстракцією - на практиці це деякі види облігаційних позик, оцінка здатності пенсійних фондів відповідати по своїх зобов’язаннях. Виходячи з суті вічної ренти, можна вважати, що її нарощена сума дорівнює нескінченно великій величині, що легко довести за формулою:

при n ®¥.

Коефіцієнт приведення для вічної ренти , звідки A=R/i, тобто сучасна величина залежить лише від величини члена ренти та прийнятої ставки відсотка.

Дата добавления: 2014-01-04