Складні відсотки

ЛЕКЦІЯ 18: ЕЛЕМЕНТИ ФІНАНСОВОЇ МАТЕМАТИКИ ТА МАТЕМАТИЧНОЇ ЕКОНОМІКИ

У практичних розрахунках в основному застосовують дискретні відсотки, тобто відсотки, що нараховуються за фіксовані однакові інтервали часу (рік, півріччя, квартал і т. ін.). Час - дискретна змінна. В деяких випадках - у доведеннях та розрахунках, пов’язаних з неперервними процесами, виникає необхідність у застосуванні неперервних відсотків. Розглянемо формулу складних відсотків:

S = P (1+ i) ⁿ. (15.1)

Тут P - початкова сума, i - ставка відсотка (у вигляді десяткового дробу), S - сума, що утворилась до кінця терміну позики в кінці n -го року. Зростання за складними відсотками являє собою процес, що розвивається за геометричною прогресією. Приєднання нарахованих відсотків до суми, яка слугувала базою для їх визначення, часто називають капіталізацією відсотків. У фінансовій практиці часто стикаються із задачею, оберненою до визначення нарощеної суми: за заданою сумою S, яку слід сплатити через деякий час n, необхідно визначити суму отриманої позики P. У цьому випадку говорять, що сума S дисконтується, а відсотки у вигляді різниці S-P називаються дисконтом. Величину P, знайдену дисконтуванням S, називають сучасною, або приведеною, величиною S. Маємо:

.

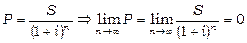Таким чином, при дуже великих термінах платежу сучасна величина останнього буде вкрай незначною.

У практичних фінансово-кредитних операціях неперервні процеси нарощення грошових сум, тобто нарощення за нескінченно малі проміжки часу, застосовуються рідко. Суттєво більше значення неперервне нарощення має у кількісному фінансово-економічному аналізі складних виробничих та господарських об’єктів та явищ, наприклад, при виборі та обґрунтуванні інвестиційних рішень. Необхідність у застосуванні неперервних нарощень (або неперервних відсотків) визначається перш за все тим, що багато економічних явищ за своєю природою неперервні, тому аналітичне описання у вигляді неперервних процесів більш адекватне, ніж на основі дискретних. Узагальнимо формулу складних відсотків для випадку, коли відсотки нараховуються m разів на рік:

S=P (1+ i/m) ^mn.

Нарощена сума при дискретних процесах знаходиться за цією формулою, тут m - число періодів нарахування в році, i - річна або номінальна ставка. Чим більше m, тим менше проміжки часу між моментами нарахування відсотків. У границі при m ®¥ маємо:

`.

Оскільки , то `.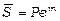

При неперервному нарощенні відсотків застосовують особливий вид процентної ставки - силу росту, яка характеризує відносний приріст нарощеної суми у нескінченно малому проміжку часу. При неперервній капіталізації відсотків нарощена сума дорівнює скінченій величині, що залежить від початкової суми, терміну нарощення та номінальної ставки відсотка. Для того, щоб відрізняти ставки неперервних відсотків від ставки дискретних відсотків, позначимо першу через d, тоді `.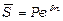

Сила росту d являє собою номінальну ставку відсотка при m ®¥. Множник нарощення розраховується за допомогою обчислювальної техніки або за таблицями функції.

Дата добавления: 2014-01-04