Статистическая оценка линейного уравнения связи

Коефіцієнт регресії.

Визначення параметрів.

Статистична оцінка лінійного рівняння зв'язку.

ЛЕКЦІЯ

до заняття №20

Тема: Рівняння лінії парної регресії.

План:

1. Статистична оцінка лінійного рівняння зв'язку.

2. Визначення параметрів 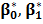. Коефіцієнт регресії.

Пусть между переменными Х и Y теоретически существует определённая линей­ная зависимость. Это утверждение может основываться на той основе, напри­мер, что корреляционное поле для пар (х_і; у_і) имеет такой вид (Рис.1).

у

0 х

Рис.1

Как видим, на самом деле между признаками Х и Y наблюдается не такая тесная связь, как это пред­полагает функциональная зависимость. Отдельные наблюдаемые значения у, как пра­вило, будут отклоняться от предполагаемой линей­ной зависимости под воздействием случайных возбу­дителей, которые в большинстве случаев неиз­вестны. Отклонение от предполагае­мой линейной формы связи может произойти в следствие непра­вильной спецификации уравнения, т.е. ещё с са­мого начала неправильно выбрано уравнение, кото­рое описывает зависимость между Х и Y.  

Будем считать, что спецификация уравнения выбрана правильно. Учитывая влия­ние на значения Y возбуждённых случайных факторов, линейное уравнение связи Х и Y можно подать в таком виде:

у_і = β₀ + β₁ х_і + 𝜀 _і, (1)

где β₀, β₁ – неизвестные параметры регрессии,

𝜀 _і – случайная переменная, которая характеризует отклонение у от гипотетиче­ской теоретической регрессии.

И так, в уравнении (1) значение «у» подаётся в виде суммы двух частей: система­тической β₀ + β₁ х_і и случайной 𝜀 _і.

Параметры β₀, β₁ являются неизвестными величинами, а 𝜀 _і – случайная вели­чина, которая имеет нормальный закон распределения с числовыми характеристиками: М(𝜀 _і ) = 0, D(𝜀 _і ) = 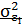= const. При этом элементы последовательности явля­ются некорелируемыми, т.е. К_ij = 0.

В результате статистических наблюдений наблюдатель получает характери­стики для независимой переменной х и соответствующие значения зависимой перемен­ной у.

И так, необходимо определить параметры β₀, β₁. Но истинные значения этих па­раметров определить невозможно, т.к. мы используем информацию, полученную из выборки ограниченного объёма.

Поэтому найденные значения параметров будут только статистическими оцен­ками истинных (неизвестных нам) параметров β₀, β₁.

Если обозначить параметры 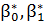, которые получили способом обработки вы­борки, модели

у_і = β₀ + β₁ х_і + 𝜀 _і, (2)

будет соответствовать статистическая оценка

у_і = 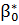+ 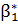х_і + 𝜀 _і. (3)

Дата добавления: 2014-01-04