
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение параметров. Коефіцієнт регресії
|
|
|
|
Если мы приняли гипотезу про линейную форму связи межу признаками Х и Y, то однозначно выбрать параметры 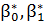 , которые есть точечными статистическими оценками соответственно для параметров β0, β1, практически невозможно. Действительно, через корреляционное поле (рис.1) можно провести множество прямых. поэтому необходимо выбрать такой критерий, по которому можно совершить выбор параметров
, которые есть точечными статистическими оценками соответственно для параметров β0, β1, практически невозможно. Действительно, через корреляционное поле (рис.1) можно провести множество прямых. поэтому необходимо выбрать такой критерий, по которому можно совершить выбор параметров 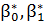 .
.
На практике чаще всего параметры 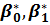 определяют по методу наименьших квадратов (разработка метода принадлежит К.Гауссу и П.Лапласу).
определяют по методу наименьших квадратов (разработка метода принадлежит К.Гауссу и П.Лапласу).
Согласно этому методу уравнение парной линейной регрессии у і = β0 + β1 х і необходимо выбрать так, чтобы сумма квадратов отклонений наблюдаемых значений от линии регрессии была бы минимальной (рис.2).

 у
у
 уі уі   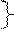  𝜀 і 𝜀 і
   
Рис.2 | Через корреляционное поле проведена линия регрессии уі = β0 + β1 хі. Отклонение любой точки с координатами (хі; уі) составляет 𝜀 і:
𝜀 і = уі – (β0 + β1 хі) (4)
уі – наблюдаемое значение признака Y, которое получили в результате реализации выборки;
β0 + β1 хі - значение признака Y, вычисленное при условии, что Х = хі.
Как видим, величина 𝜀 і является функцией от параметров 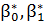 . .
|
Функция от этих параметров и будет обобщающим показателем рассеиванья точек вокруг прямой, а именно:
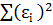 . (5)
. (5)
Отсюда есть смысл взять критерий, согласно которому параметры 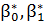 необходимо выбирать так, чтобы сумма квадратов отклонений
необходимо выбирать так, чтобы сумма квадратов отклонений 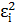 была минимальной:
была минимальной:
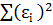 = min. (6)
= min. (6)
Обозначим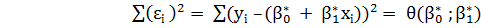 , (7)
, (7)
И рассмотрим необходимое условие существования минимума функции 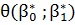 :
:
 (8)
(8)
Получим линейное уравнение относительно параметров 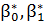 :
:
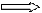


 :(-2)
:(-2) 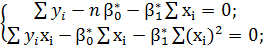


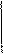

 :n
:n 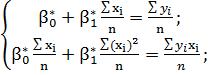
Т.к. 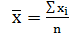 – среднее арифметическое Х;
– среднее арифметическое Х;
 – среднее арифметическое Y;
– среднее арифметическое Y;
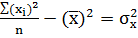 – средне квадратическое отклонение Х;
– средне квадратическое отклонение Х;
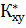 =
= 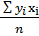 -
-  ; – эмпирический корреляционный момент;
; – эмпирический корреляционный момент;

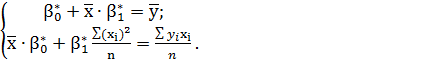 (9)
(9)
Решим систему (9) относительно параметров 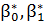 , найдём:
, найдём:
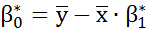 (10)
(10)
 (11)
(11)
Умножив левую и правую части равенства (11) на  , получим:
, получим:

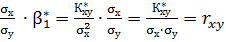
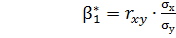 (12)
(12)
Где  – парный коэффициент корреляции между признаками Х и Y. Тогда
– парный коэффициент корреляции между признаками Х и Y. Тогда
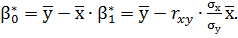 (13)
(13)
С учётом (12) и (13) уравнение линейной парной регрессии примет вид:
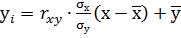 (14)
(14)
или

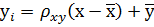 , (15)
, (15)
Где 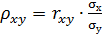 - коэффициент регрессии.
- коэффициент регрессии.
Контрольні запитання:
1. Як виглядає рівняння лінійної форми зв’язку та на які дві частини воно поділяється?
2. Що таке β0, β1 і, що таке 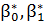 ?
?
3. Що таке 𝜀 і?
4. Як виглядає статистична оцінка рівняння лінійної форми зв’язку?
5. Який метод застосовують, щоб знайти 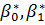 ?
?
6. Як обчислюється 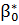 ?
?
7. Як обчислюється 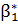 ?
?
8. Що таке  ?
?
9. Як знайти коефіцієнт регресії?
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 348; Нарушение авторских прав?; Мы поможем в написании вашей работы!





 уі β0 + β1 хі
уі β0 + β1 хі

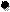
 0
0 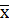 хі х
хі х