Коефіцієнт детермінації

Величину можна представити у вигляді двох складових: розрахункового значення «і» відліку та помилки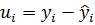

;

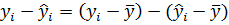, підведемо до квадрату ліву та праву частину і просумуємо їх по «і».

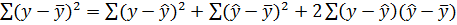: (2*)

Розглянемо вираз

Пам’ятаємо, що згідно умов Гауса-Маркова 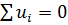, тоді вираз (2*) перетворюється в

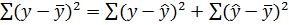(2**),

де 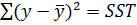– загальна сума квадратів (suma sqrt total);

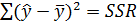– сума квадратів помилок, що пояснюється регресією (регресійна сума квадратів, suma sqrt regresic);

– сума квадратів помилок, що не пояснюється за допомогою регресії (suma sqrt error).

SST=SSR+SSE (2,3)

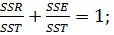(2,4)

де 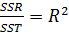– коефіцієнт детермінації.

Аналізуючи рівняння (2,4) робимо висновок, що коефіцієнт регресії завжди невід’ємний, не має одиниці виміру і не перевищує одиниці.

Ввести коефіцієнт детермінації можна іншим чином. Після побудови регресивної моделі можна записати

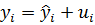
Знайдемо дисперсію у

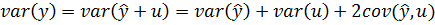
Можна довести (довести самостійно), що 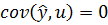. Таким чином

.

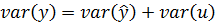Це означає, що дисперсію випадкової величини у можна розкласти на дві складові: яка «пояснюється» регресією (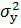) та «не пояснюється» її 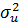. Тоді .

Зв’язок коефіцієнтів кореляції і детермінації можна виразити

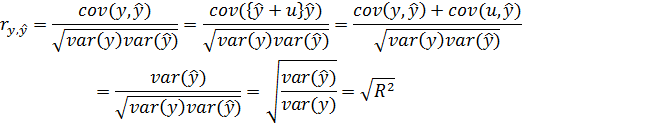
В порівнянні з коефіцієнтом кореляції коефіцієнт детермінації характеризує зв’язок незалежно від його виду: лінійний або нелінійний. Але за таку перевагу доводиться платити втратою інформації про напрямок зв’язку.

Коефіцієнт детермінації використовують тільки з позначкою «R²». Запис 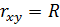не вірний, так як – це є ознака множинного коефіцієнта кореляції.

Індекс кореляції – характеризує нелінійний зв’язок між змінними

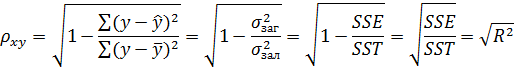
де – дисперсія «не пояснювальної» частини помилки;

– дисперсія загального (тотального) відхилення.

Тоді 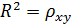. звідси, індекс кореляції не від’ємний, не має одиниць виміру і не перевищує одиниці.

Дата добавления: 2014-01-04