Элементарные преобразования

Будем делать над системами линейных уравнений элементарные преобразования трёх типов.

Будем говорить, что СЛУ S¢ получается из системы S элементарным преобразованием I-го типа (SS¢), если i- е уравнение системы S¢ получается прибавлением к i- му уравнению системы S j -го уравнения системы S, умноженного на коэффициент с Î Р (j¹ i). А все остальные уравнения системы S¢ совпадают с соответствующими уравнениями системы S. Элементарному преобразованию I-го типа системы линейных уравнений соответствует ЭП-I соответствующей расширенной матрицы, у которой при ЭП-I к i -й строке прибавляется j -я строка с коэффициентом с. Таким образом, все строки расширенной матрицы для СЛУ S¢, кроме i- й, совпадают с соответствующими строками расширенной матрицы для СЛУ S, а i- я строка имеет вид

(a_i1+ca_j1, a_i2+ca_j2,…, a_in+ca_jn,| b_i+cb_j).

При элементарном преобразовании II-го типа в системе S меняются местами i -е и j -е уравнения, а в соответствующей расширенной матрице меняются местами i -я и j -я строки.

При элементарном преобразовании III-го типа в системе S i -е уравнение умножается на коэффициент сÎ Р, с ¹ 0, а в соответствующей расширенной матрице i -я строка умножается на с.

Упражнения.

1. Доказать, что если S 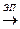S¢, то S¢ 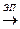S, причем обратное ЭП - того же типа.

2. Доказать, что если S 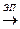S¢, то S Þ S¢ и, следовательно, S Û S¢.

На множестве СЛУ с п неизвестными введем отношение «. Пусть по определению S «S¢, если система S¢ может быть получена из S с помощью цепочки ЭП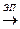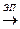: S … S¢.

Упражнения.

3. Доказать, что отношение « является отношением эквивалентности.

4. Доказать, что если S «S¢, то S Û S¢, и, следовательно, отношение эквивалентности « содержится в отношении эквивалентности Û.

Теорема. Любую матрицу размером m´n

A =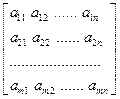

c помощью ЭП можно привести к ступенчатому виду:

= ,

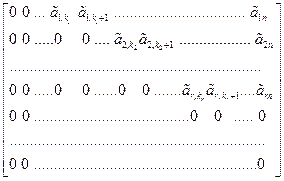где число ненулевых строк равно r, r³ 0, и все элементы 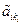¹ 0, i = 1,…,r.

Доказательство индукцией по m.

При m = 1 утверждение очевидно и ничего доказывать не надо.

Пусть для m – 1 утверждение верно. Докажем его для m. Пусть в 1-м столбце все элементы нулевые, во 2-м столбце все элементы нулевые и т.д. Пусть 1-й столбец, где встретится элемент, неравный нулю, имеет номер k₁, k₁³ 1. Строку, где находится этот ненулевой элемент, поменяем местами с 1-й строкой. Элемент, который окажется на месте с номером (1, k₁), обозначим 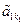, элемент, который окажется на месте с номером (1, j), обозначим 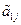, а элемент на произвольном (i, j)- м месте (i ³ 2) будем обозначать . Теперь с помощью ЭП-I сделаем нули под ненулевым элементом 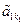. Для этого от каждой строки с номером j, j ³ 2, отнимем 1-ю строку с коэффициентом .

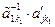После этого получим матрицу вида

.

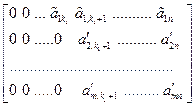Для подматрицы с m-1 строками

можно считать, что утверждение верно по предположению индукции. Отсюда и следует доказательство теоремы.



Число r ненулевых строк матрицы (число ступенек) называется рангом матрицы A и обозначается rgA. Корректность определения ранга (независимость от способа приведения A к ступенчатому виду) будет доказана позже.

Лекция 6.

Дата добавления: 2014-01-04