Определения. Свойства

На множестве квадратных (п´ п)- матриц (п = 1,2,3,…) с элементами из поля Р определим по индукции функцию det со значениями в поле Р. Значение этой функции на матрице А будем обозначать также |A| и называть определителем матрицы А.

Пусть для п = 1 для матрицы А = (а₁₁) по определению detA = а₁₁.

Далее будем считать, что для всех (п – 1)´(п – 1)- матриц функция det уже определена. Определим для (п´ п)- матрицы

A = 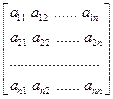функцию detA по формуле:

detA = а₁₁ M₁₁ - а₂₁ M₂₁ + а₃₁ M₃₁ - …+(-1)ⁿ⁺¹а_n1 M_n1, где M_k1 – определитель (п – 1)´(п – 1)- матрицы, которая получается из матрицы A вычеркиванием 1-го столбца и k- й строки. По предположению индукции можно считать, что все эти определители мы вычислять умеем. Определители M_k1 называются минорами, соответствующими элементам а_k1. Число п будем называть порядком (п´ п)- матрицы А, а также порядком определителя |A|.

Упражнение. Написать формулы для |A| при n = 2 и 3.

Замечание. detA можно рассматривать как функцию одного матричного аргумента A, можно рассматривать как функцию от п² аргументов а_ij, можно рассматривать как функцию от п строк матрицы A.

Обозначим i- ю строку матрицы А через А_i. То есть А_i = (а_i1 , а_i2 ,…, а_in). Рассмотрим det как функцию п строк матрицы A: detA = det (А₁ , А₂ ,…, А_n).

Утверждение 1.

det (А₁ ,…,А_i+А¢_i,…,А_n)= det (А₁ ,…,А_i,…,А_n)+ det (А₁ ,…,А¢_i,…,А_n).

Доказательство по индукции.

При п = 1 утверждение очевидно.

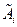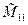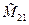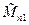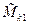Пусть утверждение верно для п – 1. Докажем его для п. Рассмотрим матрицу , у которой i- я строка = А_i+А¢_i. По определению ||= а₁₁-а₂₁+…+(-1)ⁱ⁺¹(а_i1+а¢_i1)M_i1+…+ +(-1)ⁿ⁺¹а_n1, где , k ¹ i, - миноры матрицы , M_i1 – минор матрицы А и . Так как все 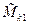- определители порядка n – 1, то по предположению индукции для них утверждение 1 верно, то есть при k ¹ i 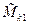= M_k1 + M¢_k1, где M_k1 - миноры для det (А₁ ,…,А_i,…,А_n), а M¢_k1 – миноры для

det (А₁ ,…,А¢_i,…,А_n). Таким образом,

||= а₁₁(M₁₁+M¢₁₁) -а₂₁(M₂₁+M¢₂₁)+…+(-1)ⁱ⁺¹(а_i1+а¢_i1)M_i1+…+ +(-1)ⁿ⁺¹а_n1 (M_n1+ M¢_n1) =

= (а₁₁M₁₁ - а₂₁M₂₁+…+(-1)ⁱ⁺¹а_i1 M_i1+…+(-1)ⁿ⁺¹а_n1M_n1)+

+ (а₁₁M¢₁₁ - а₂₁M¢₂₁+…+(-1)ⁱ⁺¹а¢_i1M_i1+…+(-1)ⁿ⁺¹а_n1 M¢_n1) =

= det (А₁ ,…,А_i,…,А_n) + det (А₁ ,…,А¢_i,…,А_n).



Утверждение 2.

det (А₁ ,…, сА_i,…, А_n) = с det (А₁ ,…, А_i,…, А_n).

Доказательство по индукции.

При п = 1 утверждение очевидно.

Пусть утверждение верно для п – 1. Докажем его для п. Рассмотрим матрицу , у которой i- я строка 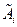= сА_i. По

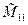определению || = а₁₁- а₂₁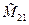+…+(-1)ⁱ⁺¹са_i1M_i1+…+

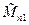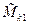+(-1)ⁿ⁺¹а_n1, где , k ¹ i, - миноры матрицы , M_i1 – минор матрицы А и . Так как все 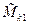- определители порядка n – 1, то по предположению индукции для них утверждение 2 верно, то есть при k ¹ i 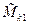= сM_k1, где M_k1 - миноры для det (А₁ ,…, А_i,…, А_n). Таким образом,

||= а₁₁сM₁₁ - а₂₁сM₂₁ +…+ (-1)ⁱ⁺¹са_i1M_i1+…+ (-1)ⁿ⁺¹а_n1сM_n1 =

= с det (А₁ ,…,А_i,…,А_n).



Свойства определителя из утверждений 1, 2 называются свойствами линейности определителя по i- й строке. Так как i – произвольная строка, i = 1¸ n, то говорят, что определи­тель - полилинейная функция строк.

Утверждение 3.

det (А₁ ,…, А_i, А_i,…, А_n) = 0 – то есть определитель, у которого две соседние строки одинаковые, равен нулю.

Доказательство по индукции.

При п = 2 утверждение очевидно из формулы для определителя 2-го порядка.

Пусть утверждение верно для п – 1. Докажем его для п. Рассмотрим матрицу А, у которой А_i+1= А_i. По определению | А | = а₁₁M₁₁ - а₂₁M₂₁+…+(-1)ⁱ⁺¹а_i1M_i1 - (-1)ⁱ⁺¹а_i1M_i1+…+

+(-1)ⁿ⁺¹а_n1M_n1, где все миноры M_k1, k ¹ i, i+1, – имеют две одинаковые соседние строки, и так как все M_k1 - определители порядка n – 1, то по предположению индукции для них утверждение 3 верно, то есть при k ¹ i, i+1 M_k1 =0. А сумма (-1)ⁱ⁺¹а_i1M_i1 - (-1)ⁱ⁺¹а_i1M_i1= 0. Таким образом, | А | = 0.



Утверждение 4.

det (А₁ ,…, А_i, А_i+1 ,…, А_n) = - det (А₁ ,…, А_i+1 , А_i,…, А_n) – то

есть если у определителя поменять местами две соседние строки, то он изменит знак.

Доказательство. Из утверждений 3 и 1

0 = det (А₁ ,…,А_i+А_i+1 ,А_i+А_i+1 ,…,А_n) = det (А₁ ,…, А_i, А_i,…, А_n)+ + det (А₁ ,…, А_i+1 , А_i,…, А_n) + det (А₁ ,…, А_i, А_i+1 ,…, А_n) +

+ det (А₁ ,…, А_i+1 , А_i+1 ,…, А_n) – в этой сумме 1-е и 4-е слагаемые по утверждению 3 равны 0, то есть

det (А₁ ,…, А_i+1 , А_i,…, А_n)+ det (А₁ ,…, А_i, А_i+1 ,…, А_n)= 0 Þ

det (А₁ ,…, А_i, А_i+1 ,…, А_n) = - det (А₁ ,…, А_i+1 , А_i,…, А_n).



Утверждение 5. Если у матрицы А при i ¹ j А_i = А_j, то

|A|= 0 – то есть определитель, у которого две строки одинаковые, равен нулю.

Доказательство. При j = i+1 определитель равен нулю по утверждению 3. Пусть j > i+1. Переставим j- ю строку с (j -1)- й, затем с (j -2)- й, с (j -3)- й и т.д. пока не дойдем до

(i + 1)- й и не получим определитель с двумя одинаковыми соседними строками – этот определитель по утверждению 3 равен нулю. Каждый раз при перестановке соседних строк по утверждению 4 определитель менял знак. После всех этих перестановок строк мы получим окончательный нулевой определитель, который отличается от нашего первоначального, может быть, разве что только знаком. Значит, и наш первоначальный определитель тоже равен нулю.



Утверждение 6.

det (А₁ ,…, А_i,…,А_j,…, А_n) = - det (А₁ ,…, А_j,…, А_i,…, А_n) – то есть если у определителя поменять местами i- ю и j -ю строки, то он изменит знак.

Доказательство аналогично доказательству утверждения 4.

Упражнение. Доказать утверждение 6.

Свойство определителя из утверждения 5 называется свойством кососимметричности (или антисимметричности) определителя по строкам.

Итак, нами доказана

Теорема. Определитель матрицы является полилиней­ной кососимметричной функцией строк этой матрицы.

Дата добавления: 2014-01-04