Упражнения. Примеры линейных пространств

Примеры линейных пространств.

Упражнения.

Определения, примеры.

ЛИНЕЙНЫЕ ПРОСТРАНСТВА

Пусть Р – произвольное поле.

Определение. Множество L называется линейным (или векторным) пространством над полем Р, если

I. на L определены бинарная операция, обозначаемая знаком +, и множество унарных операций умножения на элементы из поля Р, то есть " a, bÎ L определен результат операции

a+bÎL, и "aÎL, aÎ P определен результат операции a×aÎL, и

II. для этих операций выполнены 8 свойств:

1. (a + b)+ c = a + (b + c) " a, b, cÎ L.

2. $ элемент 0_LÎ L такой, что a + 0_L= 0_L +a = a "aÎ L.

0_L называется нейтральным элементом по сложению в L (или нейтралом по сложению или нулевым элементом). Когда ясно, о каком нулевом элементе идет речь, мы будем писать 0 без индекса L.

3. " aÎ L $ элемент a¢Î L такой, что a¢ + a = a + a¢ = 0_L.

a¢ называется элементом, противо­положным к a и обозначается -a.

4. a + b = b + a " a, b Î L,

5. a (a+b) = a a + a b " a, b Î L " a Î P,

6. (a+b) a = a a+b a, " aÎ L " a, b Î P,

7. (ab) a = a(b a) " aÎ L " a, b Î P,

8. 1 _P × a = a " aÎ L.

Элементы линейного пространства называются векторами.

Если рассматривать линейное пространство как универсальную алгебру с множеством операций W, то W = {+,-(.), 0_L,a×|_{aÎ P} }.

Определение. Подмножество L₁Í L называется подпространством линейного пространства L, если L₁ само является линейным пространством относительно тех же операций W.

1. Доказать, что L₁ - подпространство в L тогда и только тогда, когда в L₁ выполняются свойства I и II.2 из определения линейного пространства, то есть " a, bÎ L₁ a + bÎ L₁; "aÎL₁, aÎ P a×aÎL₁ ; 0_LÎ L₁.

2. Доказать, что в любом линейном пространстве L подмножества {0_L} и L являются (тривиальными) подпространствами.

1. Поле Р является линейным пространством над Р.

2. Поле является линейным пространством над любым своим подполем.

3. Множество непрерывных функций C[a,b] на отрезке [a,b] со значениями в поле R является линейным пространством над полем R.

4. Множество функций F(M) на множестве М со значениями в поле Р является линейным пространством над Р.

5. Множество многочленов Р [x] от х с коэффициентами в поле Р является линейным пространством над Р.

1. Проверить, что эти множества являются линейными пространствами.

2. Доказать, что в линейном пространстве L a× 0_L=0_L "aÎ P,

0 _P ×a = 0_L, (-1)a = - a "aÎL.

Утверждение. Множество L = Р ⁿ ={(a ₁ ,…,a _n )| все a _i Î P } является линейным пространством над полем Р.

Доказательство. I. Пусть по определению для элементов из Р ⁿ (a ₁ ,…,a _n )+ (b ₁ ,…,b _n )= (a ₁ +b ₁ ,…,a _n +b _n ),

a×(a ₁ ,…,a _n )= (a×a ₁ ,…, a×a _n ).

II. 1. Из ассоциативности сложения в P следует, что

((a ₁ ,…,a _n )+(b ₁ ,…,b _n ))+(g ₁ ,…,g _n )=((a ₁ +b ₁ )+g ₁ ,…,(a _n +b _n )+ +g _n )= (a ₁ +(b ₁ +g ₁ ),…,a _n +(b _n +g _n )) =(a ₁ ,…,a _n )+((b ₁ ,…,b _n ) + +(g ₁ ,…,g _n )).

2. Очевидно, (a ₁ ,…,a _n )+(0,…,0)= (0,…,0) + (a ₁ ,…,a _n ) =

= (a ₁ ,…,a _n ) "(a ₁ ,…,a _n )Î Р ⁿ. То есть (0,…,0)= 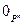- в Р ⁿ существует нейтрал по сложению.

3. Очевидно, (a ₁ ,…,a _n )+ (-a ₁ ,…,-a _n )= (0,…,0), то есть в Р ⁿ

" (a ₁ ,…,a _n ) существует противоположный элемент.

Упражнение. Доказатьсвойства 4 – 8 из определения линейного пространства.

Определения.

1. Пусть элементы a ₁ ,…,a _k Î L, a ₁ ,…,a _k Î Р. Выражение a ₁ ×a ₁ +…+a _k ×a _k называется линейной комбинацией элементов a ₁ ,…,a _k.

2. Говорят, что элементы a ₁ ,…,a _k Î L линейно зависимы, если существуют a ₁ ,…,a _k Î Р, не все равные нулю, такие, что a ₁ ×a ₁ +…+a _k ×a _k = 0 _L. Соответственно, элементы a ₁ ,…,a _k Î L линейно независимы тогда и только тогда, когда из равенства a ₁ ×a ₁ +…+a _k ×a _k = 0 _L следует, что все a _i = 0.

3. Говорят, что размерность линейного пространства L равна

п, если в L существуют п линейно независимых векторов, а

любые п+1 векторов линейно зависимы. Размерность линейного пространства L будем обозначать dim L.

4. Говорят, что размерность линейного пространства L бесконечна, если в L "п существуют п линейно независимых векторов.

5. Если dim L = п, то любые п линейно независимых векторов в L будем называть базисом линейного пространства L.

Далее, если не оговорено противное, мы будем рассматривать лишь конечномерные линейные пространства.

Дата добавления: 2014-01-04