Теоремы о базисах

Теорема 1. Пусть е ₁ ,…,е _п – базис линейного пространства L. Тогда любой вектор а Î L однозначно выражается через базис в виде а = b ₁ ×е ₁ +…+b _п ×е _п для некоторых b ₁ ,…,b _п Î Р.

Доказательство. Пусть а Î L. Так как dim L = п, то п+1 векторов а,е ₁ ,…,е _п линейно зависимы, то есть $ a,a ₁ ,…,a _п Î Р, не все равные нулю, такие, что a×а +a ₁ ×е ₁ +…+a _п ×е _п =0 _L, причем a ¹ 0, так как векторы е ₁ ,…,е _п линейно независимы. Тогда а=a ^-1a ₁ ×е ₁ +…+a ^-1a _п ×е _п =b ₁ ×е ₁ +…+b _п ×е _п, где b ₁ =a ^-1a ₁ ,…, b _п =a ^-1a _п.

Докажем однозначность. Пусть а = b ₁ ×е ₁ +…+b _п ×е _п =

= g ₁ ×е ₁ +…+g _п ×е _п Þ (b ₁ -g ₁ )е ₁ +…+(b _п -g _п )е _п = 0 _L Þ b ₁ - g ₁ =0,…, b _п -g _п = 0, так как векторы е ₁ ,…,е _п линейно независимы Þ

b ₁ = g ₁,…, b _п = g _п – это и означает однозначность.

ÿ

Теорема 2 (обратная). Пусть е ₁ ,…,е _п – такая система векторов в L, что любой вектор а Î L однозначно выражается через е ₁ ,…,е _п в виде а = b ₁ ×е ₁ +…+b _п ×е _п для некоторых

b ₁ ,…,b _п Î Р. Тогда е ₁ ,…,е _п – базис линейного пространства L.

Доказательство. 1. е ₁ ,…,е _п – линейно независимая система векторов в L, так как если a ₁ ×е ₁ +…+a _п ×е _п = 0 _L =

= 0×е ₁ +…+ 0×е _п, то из однозначности a ₁ = 0,…,a _п = 0. Следовательно, в L существуют п линейно независимых векторов.

2. Покажем, что в L любые п+1 векторов линейно зависимы.

Пусть а ₁ ,…,а _п+1 Î L. Тогда а ₁ = b ₁₁ ×е ₁ +…+b _1п ×е _п ,…,

а _п+1 =b _п+1,1 ×е ₁ +…+b _п+1,п ×е _п. Покажем, что существуют

х ₁ ,…,х _п+1 Î Р, не все равные нулю, такие, что

х ₁ а ₁ +…+х _п+1 а _п+1 = 0. Но х ₁ а ₁ +…+х _п+1 а _п+1 =

= (b ₁₁ х ₁ +…+b _п+1,1 х _п+1 )е ₁ +…+(b _1п х ₁ +…+b _п+1,п х _п+1 )е _п, и однородная система п уравнений с п+1 неизвестным

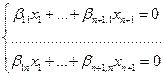имеет ненулевое решение (см. 4.3).

Таким образом, dim L = n, и е ₁ ,…,е _п – базис в L.

ÿ

Теорема 3. Если е ₁ ,…,е _п – базис линейного пространства L, то е ₁ ,…,е _п – максимальная линейно независимая система векторов в L, то есть при добавлении к этой системе любого вектора получится линейно зависимая система векторов.

Доказательство. Так как е ₁ ,…,е _п – базис, то dim L = n, и из определения размерности следует, что любые п+1 векторов линейно зависимы.

ÿ

Теорема 4 (обратная). Если е ₁ ,…,е _п – максимальная линейно независимая система векторов в L, то е ₁ ,…,е _п – базис линейного пространства L.

Доказательство. Пусть а Î L. Так как п +1 векторов а, е ₁ ,…,е _п линейно зависимы, то, как и в Теореме 1, вектор а линейно выражается через е ₁ ,…,е _п. Из линейной независимости векторов е ₁ ,…,е _п , как и в Теореме 1, следует, что выражение а через е ₁ ,…,е _п однозначно. Теперь по Теореме 2 мы получаем, что е ₁ ,…,е _п – базис линейного пространства L.

ÿ

Теорема 5. dim P ⁿ = n.

Доказательство. Пусть е ₁ =(1,0,0,…,0), е ₂ =(0,1,0,…,0),…,

е _n =(0,0,0,…,1). Тогда " (a ₁ ,a ₂ ,…,a _n )Î Р ⁿ

(a ₁ ,a ₂ ,…,a _n )= (a ₁ ,0,…,0)+ (0,a ₂ ,…,0)+ …+(0,0,…,a _n )=

=a ₁ (1,0,…,0)+ a ₂ (0,1,…,0)+ …+a _n (0,0,…,1)= a ₁ ×е ₁ +…+a _п ×е _п и это представление однозначно. Значит, по Теореме 2 е ₁ ,…,е _п – базис в P ⁿ, и dim P ⁿ = n.

ÿ

Лекция 14.

Теорема 6. Любую линейно независимую систему векторов в пространстве L можно дополнить до базиса L.

Доказательство. Пусть а ₁ ,…,а _k – линейно независимая система векторов в L. Если это максимальная линейно независимая система векторов, то а ₁ ,…,а _k – базис линейного пространства L по Теореме 4. Если это не максимальная линейно независимая система векторов, то существует некоторый вектор а _k+1 такой, что а ₁ ,…,а _k ,а _k+1 - линейно независимая система векторов в L. Опять, если это максимальная линейно независимая система векторов, то а ₁ ,…,а _k+1 – базис линейного пространства L, а если не максимальная, то добавляем вектор а _k+2 и т.д. пока не получим максимальную линейно независимую систему векторов, то есть базис.

ÿ

Пусть е ₁ ,…,е _п – базис линейного пространства L и хÎL. Тогда х = х ₁ ×е ₁ +…+х _п ×е _п, и набор (х ₁ ,…,х _п ) называется координатами вектора х в базисе е ₁ ,…,е _п .

Упражнение. Доказать, что если (х ₁ ,…,х _п ) координаты вектора х, а (у ₁ ,…,у _п ) координаты вектора у в базисе е ₁ ,…,е _п , то координатами вектора х+у будет набор (х ₁ +у ₁ ,…,х _п +у _п ), а координатами вектора a х, aÎ Р, будет набор (a х ₁ ,…,a х _п ).

Дата добавления: 2014-01-04