Подпространства

Упражнения.

1. Доказать, что L₁» L₁ (это рефлексивность изоморфизма).

2. Доказать, что если L₁» L₂ и L₂» L₃, то L₁» L₃ (это транзитивность изоморфизма).

Таким образом, отношение изоморфности между линейными пространствами рефлексивно, симметрично и транзитивно. Следовательно, все линейные пространства разбиваются на непересекающиеся классы изоморфных.

Утверждение. Если L₁» L₂, то dim L₁ = dim L₂.

Доказательство. Пусть j: L₁® L₂ - изоморфизм линейных пространств, и е₁,…,е_п – базис линейного пространства L₁. Покажем, что jе₁,…,jе_п – базис линейного пространства L₂. В самом деле, если уÎ L₂, то j ^-1уÎ L₁, j ^-1у=a ₁ ×е ₁ +…+a _п ×е _п Þ у = a ₁ jе ₁ +…+a _п jе _п . Кроме того, jе₁,…,jе_п – линейно независимы, так как если a ₁ jе ₁ +…+a _п jе _п = 0, то j(a ₁ е ₁ +…+a _п е _п ) = 0 = j (0) Þ a ₁ е ₁ +…+a _п е _п = 0 (из инъективности j) Þ a ₁ =…=a _п = 0.

Таким образом, любой вектор из L₂ представляется в виде линейной комбинации векторов jе₁,…,jе_п, и из их линейной независимости следует, что это представление однозначно (см. Теорему 1). Из Теоремы 2 следует, что jе₁,…,jе_п – базис в L₂.

ÿ

Теорема. Если dim L = n, то L» P ⁿ.

Доказательство. Пусть dim L = n, и е₁,…,е_п – базис в L. Рассмотрим j: L ® P ⁿ такое, что " х = х ₁ е ₁ +…+х _п е _п Î L j х= (х ₁ ,…,х _п )Î P ⁿ. Из однозначности представления х в виде х = х ₁ е ₁ +…+х _п е _п следует, что j определено корректно. Биективность j очевидна. Линейность j требовалось доказать в упражнении в 7.2.

ÿ

Следствие. Все пространства одной размерности изоморфны. И значит, пространства изоморфны тогда и только тогда, когда у них одинаковая размерность. Таким образом, класс изоморфных друг другу пространств полностью задается размерностью любого из этих пространств. И для любой размерности п с точностью до изоморфизма существует лишь одно пространство размерности п. Например, пространство P ⁿ. Все остальные пространства размерности п ему изоморфны.

Пусть L - п -мерное линейное пространство над полем Р (так как L» P ⁿ, то, не теряя общности, можно было бы считать, что L = P ⁿ).

Утверждение. Пересечение любого семейства подпространств в L является подпространством.

Доказательство. Пусть L_i,iÎ I, - подпространства в L, где I – некоторое множество индексов, L¢ = . Докажем, что L¢ - подпространство в L.

I. Пусть х, уÎ L¢ Þ х, уÎ L_i " iÎ I Þ х+ у, a хÎ L_i " iÎ I, "aÎ P Þ х+ у, a хÎ = L¢.

II.2. Так как 0_L Î L_i " iÎ I Þ 0_L Î= L¢.

ÿ

Утверждение. Пусть L₁, L₂ – подпространства, и L₁Í L₂.

Тогда dimL₁£ dimL₂, и если dimL₁= dimL₂, то L₁= L₂.

Доказательство. Пусть L₁Í L₂. Тогда базис подпространства L₁ является линейно независимой системой векторов в L₂ , и её можно дополнить до базиса L₂ . И значит, число векторов в базисе L₂ не меньше, чем число векторов в базисе L₁, то есть dimL₁£ dimL₂. Если же dimL₁= dimL₂, то любой базис подпространства L₁ является базисом подпространства L₂, и любой вектор из L₂, являясь линейной комбинацией базисных векторов, содержится в L₁. Следовательно, L₂Í L₁Þ L₂= L₁.

ÿ

Рассмотрим способы задания подпространств в L.

Определение. Пусть векторы а₁,…,а_mÎL. Линейной оболочкой системы векторов {а₁,…,а_m} называется ³⁾наименьшее ¹⁾подпространство в L, ²⁾содержащее векторы а₁,…,а_m. Эту линейную оболочку мы будем обозначать <а₁,…,а_m>.

В нашем определении для линейной оболочки требуется выполнение трех условий: 1) <а₁,…,а_m> - подпространство, 2) это подпространство должно содержать векторы а₁,…,а_m, 3) среди всех таких подпространств линейная оболочка – наименьшее (по включению) подпространство, то есть содержится в любом другом подпространстве, для которого выполняются условия 1), 2).

Покажем, что линейная оболочка системы векторов существует.

Утверждение. Линейная оболочка системы векторов {а₁,…,а_m} равна пересечению всех подпространств из L, содержащих эти векторы.

Доказательство. Очевидно, множество таких подпространств не пусто, так как содержит тривиальное подпространство L. Далее, ¹⁾пересечение всех таких подпространств – подпространство, ²⁾содержащее векторы {а₁,…,а_m}. И наконец, ³⁾это подпространство - наименьшее, так как пересечение подмножеств содержится в любом из пересекающихся подмножеств.

ÿ

Утверждение. <а₁,…,а_m>= {a ₁ a ₁ +…+a _m a _m |a ₁ ,…,a _m Î P }, то есть линейная оболочка системы векторов {а₁,…,а_m} равна множеству всевозможных линейных комбинаций векторов {а₁,…,а_m}.

Доказательство. ¹⁾Докажем, что V = {a ₁ a ₁ +…+a _m a _m |a ₁ ,…,a _m Î P } – подпространство.

I. Пусть х, у Î V, x = a ₁ a ₁ +…+a _m a _m, y = b ₁ a ₁ +…+b _m a _m Þ x+y=(a ₁ +b ₁ )a ₁ +…+(a _m +b _m )a _m , ax= (aa ₁ )a ₁ +…+(aa _m )a _m Î V.

II.2. 0 = 0a ₁ +…+0a _m Î V.

²⁾Очевидно, а₁ = 1×а₁ + 0×а₂ +…+ 0×а_m Î V. Аналогично, а₂,…, а_mÎ V.

³⁾Пусть подпространство W' а₁, а₂ ,…, а_m Þ все a ₁ a ₁ +…+a _m a _m Î W Þ VÍ W.

Следовательно, V – наименьшее подпространство, содержащее векторы а₁, а₂ ,…, а_m Þ V = <а₁,…,а_m>.

ÿ

Определение. Если V = <а₁,…,а_m>, то векторы а₁,…,а_m называются образующими подпространства V.

В этом случае любой вектор из V представляется в виде линейной комбинации системы образующих. Если к тому же векторы а₁,…,а_m линейно независимы, то такое представление однозначно, и система образующих является базисом линейного пространства V.

Лекция 15.

Определение. Рангом системы векторов {а₁,…,а_m} называется число rg {а₁,…,а_m} = dim<а₁,…,а_m>.

По аналогии с элементарными преобразованиями строк матрицы или системы линейных уравнений (см. 4.2) определим элементарные преобразования (ЭП) системы векторов S = {а₁,…,а_m}.

Определение. Будем говорить, что система векторов S¢ получается из системы векторов S элементарным преобразованием I-го типа (SS¢), если i- й вектор системы S¢ получается прибавлением к i- му вектору системы S j -го вектора системы S, умноженного на коэффициент сÎ Р (j¹ i). А все остальные векторы системы S¢ совпадают с соответствующими векторами системы S.

При элементарном преобразовании II-го типа в системе S меняются местами i -й и j -й векторы.

При элементарном преобразовании III-го типа в системе S i -й вектор умножается на коэффициент сÎ Р, с ¹ 0.

Если координаты системы векторов записывать по строкам матрицы, то при элементарных преобразованиях системы векторов происходят такие же элементарные преобразования со строками матрицы.

Упражнение. Доказать, что если S 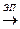S¢, то S¢ 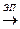S, причем обратное ЭП - того же типа.

Докажем, что при элементарных преобразованиях не меняется линейная оболочка системы векторов и, следовательно, ранг системы векторов, то есть если S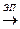S¢, то <S>=< S¢> и rg S = rg S¢.

Утверждение. Если S 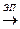S¢, то < S¢>Í <S>.

Доказательство. Так как S¢ содержится в подпространстве <S>, то подпространство <S¢>- наименьшее подпространство, содержащее S¢ - содержится в <S>, то есть < S¢>Í <S>.

Следствие. Если S S¢, то < S¢>Í <S>, и S¢ S, то есть < S>Í <S¢>, и значит, <S>=< S¢>, и rg S = rg S¢.

Покажем, как находить ранг системы векторов S. Пусть S = {а₁,…,а_m}, и в координатах a_i = (a_i1, …,a_in), i =1,…,m.

Запишем координаты векторов из S по строкам матрицы A, и будем делать над этими строками элементарные преобразования так (см. 4.2), чтобы привести эту матрицу к ступенчатому виду

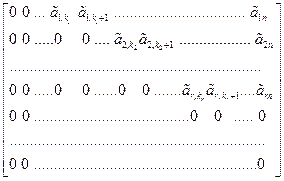= , где число ненулевых строк равно r, r³ 0, и все элементы 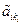¹ 0, i = 1,…,r.

Полученную соответствующую систему векторов обозначим

= {}, где . Очевидно, <S> = <>= = <>= 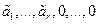{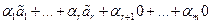|a_iÎ P }=

= <>. Покажем, что векторы линейно независимы. Пусть . Приравнивая координаты с номером k₁ в левой и правой частях равенства, получим = 0 Þ b₁= 0. Затем приравняем координаты с номером k₂ в левой и правой частях равенства и получим = 0 Þ b₂= 0. Далее переходим к координате с номером k₃ и т.д. Таким образом, мы получим, что b₁=…=b_r = 0, векторы линейно независимы, то есть являются базисом в <> и в <S>. И значит, dim<S>= dim<>= rg S = rg = r.

Отсюда следует корректность определения ранга в 4.2 – так как r = dim<S>, то r не зависит от способа приведения матрицы к ступенчатому виду.

Дата добавления: 2014-01-04