Определитель произведения матриц

Упражнения.

Элементарные матрицы.

В соответствии с определением элементарных преобразований I-го, II-го и III-го типа над строками или столбцами матрицы определим элементарные матрицы I-го, II-го и III-го типа.

Определение. Элементарной матрицей I-го типа называется (п,п)- матрица Р_i,j(с) = Е + сE_i,j, i ¹ j.

Элементарной матрицей II-го типа называется (п,п)- матрица Р_i,j= E_1,1 + E_2,2+…+ E_i-1,i-1+ E_i,j+ E_i+1,i+1+…+E_j-1,j-1+E_j,i + E_j+1,j+1+

+…+ E_n,n = E - E_i,i - E_j,j + E_i,j + E_j,i, при i ¹ j.

Элементарной матрицей III-го типа называется диагональная (п,п)- матрица Р_i (c) = diag(1,1,…,c,…,1) =

= E_1,1 + E_2,2 + … + cE_i,i + … + E_n,n = Е + (с – 1)E_i,i, где с ¹ 0.

1. Проверить, что при умножении произвольной (п,т)- матрицы А слева на элементарную (п,п)- матрицу Р_i,j(с) у матрицы А к i- й строке прибавляется j- я строка с коэффициентом с, при умножении А слева на Р_i,j у матрицы А меняются местами i- я и j- я строки, при умножении А слева на Р_i (с) у матрицы А i- я строка умножается на с ¹ 0. Таким образом, при умножении матрицы А слева на элементарную матрицу s-го типа (s = I, II, III) над строками матрицы А происходит элементарное преобразование того же s-го типа.

2. Проверить, что при умножении произвольной (т,п)- матрицы А справа на элементарную (п,п)- матрицу Р_i,j(с) у матрицы А к j- му столбцу прибавляется i- й столбец с коэффициентом с, при умножении А справа на Р_i,j у матрицы А меняются местами i- й и j- й столбцы, при умножении А справа на Р_i (с) у матрицы А i- й столбец умножается на с. Таким образом, при умножении матрицы А справа на элементарную матрицу s-го типа над столбцами матрицы А происходит элементарное преобразование того же s-го типа.

Теорема. Пусть А, ВÎ М_п(Р). Тогда |A×B| = |A|× |B|.

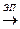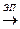
Доказательство. С помощью элементарных преобразований I-го и II-го типа над строками матрицы А (см. Теорему из 4.2) приведем её к ступенчатому виду: А… . Каждому ЭП над строками матрицы соответствует умножение этой матрицы на соответствующую элементарную матрицу слева. Таким образом, существуют элементарные матрицы Р₁, Р₂,…,P_k такие, что P_k … Р₂Р₁А = . Очевидно, || = (-1)^s|A|, где s – количество элементарных матриц II-го типа среди Р₁, Р₂ ,…,P_k. Рассмотрим два случая.

1. |A| = 0. Тогда последняя строка матрицы - нулевая, и значит, последняя строка матрицы В – также нулевая. Следовательно, 0 = | В| = |P_k … Р₂Р₁АB| = (-1)^s|AB| Þ |AB| = 0 = =|A|× |B|. В этом случае утверждение доказано.

2. |A| ¹ 0. В этом случае последняя строка матрицы - ненулевая, и матрица - треугольная. Далее как в 4.4, начиная с последней строки, с помощью только ЭП-I над строками можно сделать над каждым диагональным элементом нули, то есть получить диагональную матрицу D = diag(d₁,…,d_n):

…D. Значит, существуют элементарные матрицы I-го типа Q₁, Q₂,…,Q_t такие, что Q_t … Q₂Q₁ = D,

Q_t … Q₂Q₁P_k … Р₂Р₁А= D, и | A|= (-1)^s| | = (-1)^s|D|=(-1)^sd₁,…,d_n. Но при умножении матрицы В на D слева 1-я строка матрицы В умножается на d₁, 2-я строка матрицы В умножается на d₂ и т.д., то есть | DB| =d₁,…,d_n | B| = | D||B|. Следовательно,

| AB|=(-1)^s|Q_t … Q₂Q₁P_k … Р₂Р₁АB|=(-1)^s|DB|=(-1)^s|D||B| = | A||B|.

Таким образом, в случае 2 утверждение также доказано.

ÿ

Лекция 19.

Дата добавления: 2014-01-04