Матрица линейного отображения

Простейшие свойства линейных отображений.

1. j(0_L)= 0_L¢, но в общем случае j ^-1(0_L¢)¹ 0_L, хотя

j ^-1(0_L¢)' 0_L – см. примеры 1- 4.

1. j(-a) = - j a "a Î L.
2. j()= .

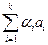Действительно, j(0_L) = j(0×0_L) = 0×j(0_L) = 0,

j(-a)= j((-1)×a)= (-1)×j a = - j a, а свойство 3 доказывается индукцией по k.

Упражнение. Найти j ^-1(0_L¢) в примерах 1-5.

Пусть Lⁿ, L^m - линейные пространства над полем P,

j: Lⁿ ® L^m - линейное отображение, e ={e₁, …,e_n} - произволь­ный базис в Lⁿ.

Лемма 1. Линейное отображение j: Lⁿ ® L^m полностью и однозначно определяется образами базисных векторов

j e₁,…,j e_n.

Доказательство. Пусть x ÎLⁿ, x =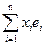. Тогда

j x = j(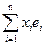)= 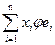Þ " xÎLⁿ jx определяется векторами j e₁,…,j e_n причем однозначно.



Пусть j: Lⁿ ® L^m - линейное отображение, e ={e₁, …,e_n} –

базис в Lⁿ, e¢ ={e¢₁, …,e¢_m} – базис в L^m. Выразим векторы j e_j через базис e¢. Пусть j e_j =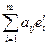, j=1,…,n. Матрицу

(a_ij) размером m´n будем называть матрицей линей­ного

отображения j в базисах e и e¢ и обозначать 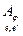, или 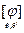, или [ j ], если ясно, какие базисы имеются ввиду. Очевидно, 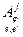= [ 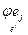], то есть j- й столбец матрицы 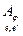- это столбец координат вектора j e_j в базисе e¢. Единственность матрицы линейного отображения j при фиксированных базисах e и e¢ следует из леммы 1 и единственности координат вектора в данном базисе.

Упражнение. Найти матрицы линейных отображений в примерах 1-5.

Замечание. Пусть по определению [ x ] = [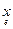] = - столбец координат вектора x в базисе e. Если допустить умножение векторов на элементы поля справа, положив по определению а×a = a×а "aÎ Р, "аÎL (проверить корректность!), то можно написать в матричном виде следующие равенства:

х = e₁х₁+…+e_nх_n = (e₁, …,e_n)× [ х ] = e × [ х ], (13.1)

(je₁, …,je_n) = (e¢₁, …,e¢_m)× [ j ] или j е = е¢ × [ j ].

Лемма 2. Пусть e ={e₁, …,e_n} – базис в Lⁿ, {a₁, …,a_n} – про­извольная система векторов в L^m. Тогда $! линейное отобра-­

жение j: Lⁿ ® L^m такое, что j e_i= a_i, i=1,…,n.

Дата добавления: 2014-01-04